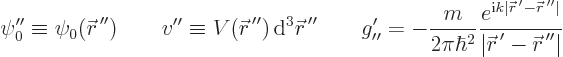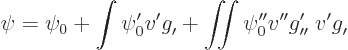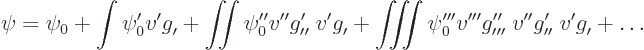| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
A.31 The Born series
The Born approximation is concerned with the problem of a particle of
a given momentum that is slightly perturbed by a nonzero potential
that it encounters. This note gives a description how this problem
may be solved to high accuracy. The solution provides a model for the
so-called Feynman diagrams
of quantum electrodynamics.
It is assumed that in the absence of the perturbation, the wave
function of the particle would be
In this state, the particle has a momentum 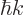 that is purely
in the
that is purely
in the  -direction. Note that the above state is not normalized,
and cannot be. That reflects the Heisenberg uncertainty principle:
since the particle has precise momentum, it has infinite uncertainty
in position. For real particles, wave functions of the form above
must be combined into wave packets, chapter 7.10. That
is not important for the current discussion.
-direction. Note that the above state is not normalized,
and cannot be. That reflects the Heisenberg uncertainty principle:
since the particle has precise momentum, it has infinite uncertainty
in position. For real particles, wave functions of the form above
must be combined into wave packets, chapter 7.10. That
is not important for the current discussion.
The perturbed wave function  can in principle be obtained
from the so-called integral Schrödinger equation, {A.13}
(A.42):
can in principle be obtained
from the so-called integral Schrödinger equation, {A.13}
(A.42):
Evaluating the right hand side in this equation would give
 . Unfortunately, the right hand side cannot be evaluated
because the integral contains the unknown wave function
. Unfortunately, the right hand side cannot be evaluated
because the integral contains the unknown wave function  still
to be found. However, Born noted that if the perturbation is small,
then so is the difference between the true wave function
still
to be found. However, Born noted that if the perturbation is small,
then so is the difference between the true wave function  and
the unperturbed one
and
the unperturbed one 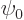 . So a valid approximation to the
integral can be obtained by replacing
. So a valid approximation to the
integral can be obtained by replacing  in it by the known
in it by the known
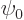 . That is certainly much better than just leaving the
integral away completely, which would give
. That is certainly much better than just leaving the
integral away completely, which would give 

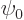 .
.
And note that you can repeat the process. Since you now have an
approximation for  that is better than
that is better than 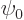 , you can
put that approximation into the integral instead. Evaluating the
right hand side then produces a still better approximation for
, you can
put that approximation into the integral instead. Evaluating the
right hand side then produces a still better approximation for
 . Which can then be put into the integral. Etcetera.
. Which can then be put into the integral. Etcetera.
Figure A.22:
Graphical interpretation of the Born series.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(400,70...
...'$}}
\put(388,30){\makebox(0,0)[r]{$+\quad\ldots$}}
\end{picture}
\end{figure}](img5146.gif) |
Graphically, the process is illustrated in figure A.22. The
most inaccurate approximation is to take the perturbed wave function
as the unperturbed wave function at the same position  :
:
An improvement is to add the integral evaluated using the unperturbed
wave function:
To represent this concisely, it is convenient to introduce some
shorthand notations:
Using those notations the improved approximation to the wave function
is
Note what the second term does: it takes the unperturbed wave function
at some different location 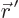 , multiplies it by a
, multiplies it by a
vertex factor
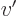 , and then adds it to the wave
function at
, and then adds it to the wave
function at  multiplied by a
multiplied by a propagator
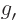 . This is then summed over all
locations
. This is then summed over all
locations 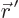 . The second term is illustrated in the
second graph in the right hand side of figure A.22.
. The second term is illustrated in the
second graph in the right hand side of figure A.22.
The next better approximation is obtained by putting the two-term
approximation above in the integral:
where
Note that it was necessary to change the notation for one integration
variable to 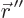 to avoid using the same symbol for two different
things. Compared to the previous approximation, there is now a third
term:
to avoid using the same symbol for two different
things. Compared to the previous approximation, there is now a third
term:
This third term takes the unperturbed wave function at some position
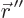 , multiplies it by the local vertex factor
, multiplies it by the local vertex factor 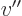 ,
propagates that to a location
,
propagates that to a location 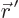 using propagator
using propagator
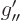 , multiplies it by the vertex factor
, multiplies it by the vertex factor
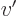 , and propagates it to the location
, and propagates it to the location  using propagator
using propagator
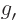 . That is summed over all
combinations of locations
. That is summed over all
combinations of locations 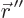 and
and 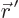 . The idea is
shown in the third graph in the right hand side of figure
A.22.
. The idea is
shown in the third graph in the right hand side of figure
A.22.
Continuing this process produces the Born series:
The Born series inspired Feynman to formulate relativistic quantum
mechanics in terms of vertices connected together into “Feynman diagrams.” Since there is a nontechnical, very readable
discussion available from the master himself, [19], there
does not seem much need to go into the details here.
![]()
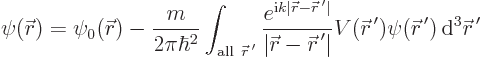
![]()
![]() ,
,![]() .
.![]() :
: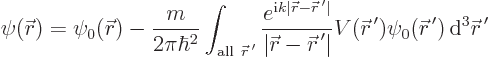
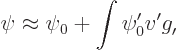
![\begin{displaymath}
\psi \approx \psi_0 + \int
\left[\psi_0' + \int \psi_0'' v...
...rime\prime}^{\prime}\right]
v' g_{\prime}^{\vphantom{\prime}}
\end{displaymath}](img5154.gif)