7.11 Al­most Clas­si­cal Mo­tion

This sec­tion ex­am­ines the mo­tion of a par­ti­cle in the pres­ence of a sin­gle ex­ter­nal force. Just like in the pre­vi­ous sec­tion, it will be as­sumed that the ini­tial po­si­tion and mo­men­tum are nar­rowed down suf­fi­ciently that the par­ti­cle is re­stricted to a rel­a­tively small, co­her­ent, re­gion. So­lu­tions of this type are called “wave pack­ets.”

In ad­di­tion, for the ex­am­ples in this sec­tion the forces vary slowly enough that they are ap­prox­i­mately con­stant over the spa­tial ex­tent of the wave packet. Hence, ac­cord­ing to Ehren­fest's the­o­rem, sec­tion 7.2.1, the wave packet should move ac­cord­ing to the clas­si­cal New­ton­ian equa­tions.

The ex­am­ples in this sec­tion were ob­tained on a com­puter, and should be nu­mer­i­cally ex­act. De­tails about how they were com­puted can be found in ad­den­dum {A.27}, if you want to un­der­stand them bet­ter, or cre­ate some your­self.

There is an easy gen­eral way to find ap­prox­i­mate en­ergy eigen­func­tions and eigen­val­ues ap­plic­a­ble un­der the con­di­tions used in this sec­tion. It is called the WKB method. Ad­den­dum {A.28} has a de­scrip­tion.

7.11.1 Mo­tion through free space

First con­sider the triv­ial case that there are no forces; a par­ti­cle in free space. This will pro­vide the ba­sis against which the mo­tion with forces in the next sub­sec­tions can be com­pared to.

Clas­si­cally, a par­ti­cle in free space moves at a con­stant ve­loc­ity. In quan­tum me­chan­ics, the wave packet does too; fig­ure 7.15 shows it at two dif­fer­ent times.

Fig­ure 7.15: A par­ti­cle in free space.

 

Move your mouse over ei­ther fig­ure to see the an­i­ma­tion. Javascript must be en­abled on your browser. Give it a few sec­onds for the an­i­ma­tion to load, es­pe­cially on a phone line.
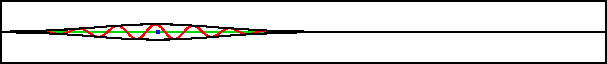
Im­proved res­o­lu­tion ver­sion (526 kB)

If you step back far enough that the wave packet in the fig­ures be­gins to re­sem­ble just a dot, you have clas­si­cal mo­tion. The blue point in­di­cates the po­si­tion of max­i­mum wave func­tion mag­ni­tude, as a vi­sual an­chor. It pro­vides a rea­son­able ap­prox­i­ma­tion to the ex­pec­ta­tion value of po­si­tion when­ever the wave packet con­tour is more or less sym­met­ric. A closer ex­am­i­na­tion shows that the wave packet is ac­tu­ally chang­ing a bit in size in ad­di­tion to trans­lat­ing.

7.11.2 Ac­cel­er­ated mo­tion

Fig­ure 7.16 shows the mo­tion when the po­ten­tial en­ergy (shown in green) ramps down start­ing from the mid­dle of the plot­ted range. Phys­i­cally this cor­re­sponds to a con­stant ac­cel­er­at­ing force be­yond that point. A clas­si­cal point par­ti­cle would move at con­stant speed un­til it en­coun­ters the ramp, af­ter which it would start ac­cel­er­at­ing at a con­stant rate. The quan­tum me­chan­i­cal so­lu­tion shows a cor­re­spond­ing ac­cel­er­a­tion of the wave packet, but in ad­di­tion the wave packet stretches a lot.

Fig­ure 7.16: An ac­cel­er­at­ing par­ti­cle.

 

Move your mouse over the bot­tom fig­ure to see the an­i­ma­tion. Javascript must be en­abled on your browser. Give it a few sec­onds for the an­i­ma­tion to load, es­pe­cially on a phone line.
Im­proved res­o­lu­tion ver­sion (564 kB)

7.11.3 De­cel­er­ated mo­tion

Fig­ure 7.17 shows the mo­tion when the po­ten­tial en­ergy (shown in green) ramps up start­ing from the cen­ter of the plot­ting range. Phys­i­cally this cor­re­sponds to a con­stant de­cel­er­at­ing force be­yond that point. A clas­si­cal point par­ti­cle would move at con­stant speed un­til it en­coun­ters the ramp, af­ter which it would start de­cel­er­at­ing un­til it runs out of ki­netic en­ergy; then it would be turned back, re­turn­ing to where it came from.

The quan­tum me­chan­i­cal so­lu­tion shows a cor­re­spond­ing re­flec­tion of the wave packet back to where it came from. The black dot on the po­ten­tial en­ergy line shows the “turn­ing point” where the po­ten­tial en­ergy be­comes equal to the nom­i­nal en­ergy of the wave packet. That is the point where clas­si­cally the par­ti­cle runs out of ki­netic en­ergy and is turned back.

Fig­ure 7.17: A de­cel­er­at­ing par­ti­cle.

 

Move your mouse over the bot­tom fig­ure to see the an­i­ma­tion. Javascript must be en­abled on your browser. Give it a few sec­onds for the an­i­ma­tion to load, es­pe­cially on a phone line.
Im­proved res­o­lu­tion ver­sion (895 kB)

7.11.4 The har­monic os­cil­la­tor

The har­monic os­cil­la­tor de­scribes a par­ti­cle caught in a force field that pre­vents it from es­cap­ing in ei­ther di­rec­tion. In all three pre­vi­ous ex­am­ples the par­ti­cle could at least es­cape to­wards the far left. The har­monic os­cil­la­tor was the first real quan­tum sys­tem that was solved, in chap­ter 4.1, but only now, near the end of part I, can the clas­si­cal pic­ture of a par­ti­cle os­cil­lat­ing back and for­ward ac­tu­ally be cre­ated.

There are some math­e­mat­i­cal dif­fer­ences from the pre­vi­ous cases, be­cause the en­ergy lev­els of the har­monic os­cil­la­tor are dis­crete, un­like those of the par­ti­cles that are able to es­cape. But if the en­ergy lev­els are far enough above the ground state, lo­cal­ized wave pack­ets sim­i­lar to the ones in free space may be formed, {A.27}. The an­i­ma­tion in fig­ure 7.18 gives the mo­tion of a wave packet whose nom­i­nal en­ergy is hun­dred times the ground state en­ergy.

Fig­ure 7.18: Un­steady so­lu­tion for the har­monic os­cil­la­tor. The third pic­ture shows the max­i­mum dis­tance from the nom­i­nal po­si­tion that the wave packet reaches.

 

Move your mouse over any fig­ure to see the an­i­ma­tion. Javascript must be en­abled on your browser. Give it a few sec­onds for the an­i­ma­tion to load, es­pe­cially on a phone line.
Im­proved res­o­lu­tion ver­sion (1,021 kB)

The wave packet per­forms a pe­ri­odic os­cil­la­tion back and forth just like a clas­si­cal point par­ti­cle would. In ad­di­tion, it os­cil­lates at the cor­rect clas­si­cal fre­quency $\omega$. Fi­nally, the point of max­i­mum wave func­tion, shown in blue, fairly closely obeys the clas­si­cal lim­its of mo­tion, shown as black dots.

Cu­ri­ously, the wave func­tion does not re­turn to the same val­ues af­ter one pe­riod: it has changed sign af­ter one pe­riod and it takes two pe­ri­ods for the wave func­tion to re­turn to the same val­ues. It is be­cause the sign of the wave func­tion can­not be ob­served phys­i­cally that clas­si­cally the par­ti­cle os­cil­lates at fre­quency $\omega$, and not at $\frac12\omega$ like the wave func­tion does.

Key Points

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

When the forces change slowly enough on quan­tum scales, wave pack­ets move just like clas­si­cal par­ti­cles do.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

Ex­am­ined in de­tail, wave pack­ets may also change shape over time.