| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.12 The harmonic oscillator solution
If you really want to know how the harmonic oscillator wave function
can be found, here it is. Read at your own risk.
The ODE (ordinary differential equation) to solve is
where the spring constant 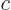 was rewritten as the equivalent
expression
was rewritten as the equivalent
expression 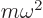 .
.
Now the first thing you always want to do with this sort of problems
is to simplify it as much as possible. In particular, get rid of as
much dimensional constants as you can by rescaling the variables:
define a new scaled  -coordinate
-coordinate 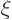 and a scaled energy
and a scaled energy
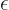 by
by
If you make these replacements into the ODE above, you can make the
coefficients of the two terms in the left hand side equal by choosing
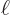

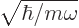 . In that case both terms
will have the same net coefficient
. In that case both terms
will have the same net coefficient 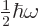 . Then
if you cleverly choose
. Then
if you cleverly choose 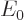

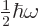 , the
right hand side will have that coefficient too, and you can divide it
away and end up with no coefficients at all:
, the
right hand side will have that coefficient too, and you can divide it
away and end up with no coefficients at all:
Looks a lot cleaner, not?
Now examine this equation for large values of 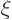 (i.e. large
(i.e. large  ).
You get approximately
).
You get approximately
If you write the solution as an exponential, you can ballpark that it
must take the form
where the dots indicate terms that are small compared to
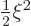 for large
for large 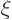 . The form of the solution is
important, since
. The form of the solution is
important, since 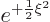 becomes infinitely large at large
becomes infinitely large at large
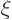 . That is unacceptable: the probability of finding the
particle cannot become infinitely large at large
. That is unacceptable: the probability of finding the
particle cannot become infinitely large at large  : the total
probability of finding the particle must be one, not infinite. The
only solutions that are acceptable are those that behave as
: the total
probability of finding the particle must be one, not infinite. The
only solutions that are acceptable are those that behave as
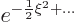 for large
for large 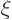 .
.
Now split off the leading exponential part by defining a new unknown
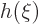 by
by
Substituting this in the ODE and dividing out the exponential, you
get:
Now try to solve this by writing 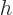 as a power series, (say, a Taylor
series):
as a power series, (say, a Taylor
series):
where the values of  run over whatever the appropriate powers are
and the
run over whatever the appropriate powers are
and the 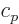 are constants. If you plug this into the ODE, you get
are constants. If you plug this into the ODE, you get
For the two sides to be equal, they must have the same coefficient for
every power of 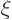 .
.
There must be a lowest value of  for which there is a nonzero
coefficient
for which there is a nonzero
coefficient 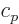 , for if
, for if  took on arbitrarily large negative
values,
took on arbitrarily large negative
values, 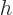 would blow up strongly at the origin, and the probability
to find the particle near the origin would then be infinite. Denote
the lowest value of
would blow up strongly at the origin, and the probability
to find the particle near the origin would then be infinite. Denote
the lowest value of  by
by 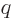 . This lowest power produces a
power of
. This lowest power produces a
power of 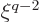 in the left hand side of the equation above, but
there is no corresponding power in the right hand side. So, the
coefficient
in the left hand side of the equation above, but
there is no corresponding power in the right hand side. So, the
coefficient 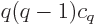 of
of 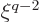 will need to be zero, and that
means either
will need to be zero, and that
means either 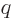
 0 or
0 or 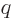
 1. So the power series for
1. So the power series for 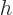 will need to start as either
will need to start as either 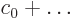 or
or 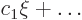 .
The constant
.
The constant 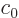 or
or 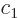 is allowed to have any nonzero value.
is allowed to have any nonzero value.
But note that the 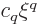 term normally produces a term
term normally produces a term
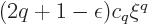 in the right hand side of the equation
above. For the left hand side to have a matching
in the right hand side of the equation
above. For the left hand side to have a matching 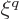 term, there
will need to be a further
term, there
will need to be a further 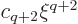 term in the power series
for
term in the power series
for 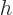 ,
,
where 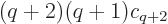 will need to equal
will need to equal
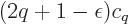 , so
, so 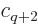

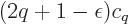

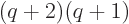 . This term in turn will
normally produce a term
. This term in turn will
normally produce a term 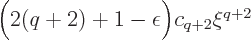 in the right hand side which will have to be canceled in the left
hand side by a
in the right hand side which will have to be canceled in the left
hand side by a 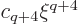 term in the power series for
term in the power series for
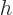 . And so on.
. And so on.
So, if the power series starts with 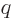
 0, the solution will take the
general form
0, the solution will take the
general form
while if it starts with 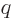
 1 you will get
1 you will get
In the first case, you have a symmetric solution, one which remains
the same when you flip over the sign of 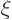 , and in the second
case you have an antisymmetric solution, one which changes sign when
you flip over the sign of
, and in the second
case you have an antisymmetric solution, one which changes sign when
you flip over the sign of 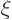 .
.
You can find a general formula for the coefficients of the series by
making the change in notations 

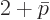 in the left-hand-side sum:
in the left-hand-side sum:
Note that you can start summing at 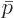

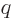 rather than
rather than
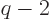 , since the first term in the sum is zero anyway. Next
note that you can again forget about the difference between
, since the first term in the sum is zero anyway. Next
note that you can again forget about the difference between 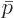 and
and  , because it is just a symbolic summation variable. The
symbolic sum writes out to the exact same actual sum whether you call
the symbolic summation variable
, because it is just a symbolic summation variable. The
symbolic sum writes out to the exact same actual sum whether you call
the symbolic summation variable  or
or 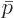 .
.
So for the powers in the two sides to be equal, you must have
In particular, for large  , by approximation
, by approximation
Now if you check out the Taylor series of 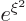 , (i.e.
the Taylor series of
, (i.e.
the Taylor series of 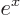 with
with  replaced by
replaced by 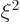 ,) you
find it satisfies the exact same equation. So, normally the solution
,) you
find it satisfies the exact same equation. So, normally the solution
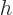 blows up something like
blows up something like 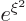 at large
at large 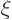 . And
since
. And
since 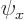 was
was 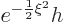 , normally
, normally 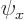 takes
on the unacceptable form
takes
on the unacceptable form 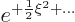 . (If you
must have rigor here, estimate
. (If you
must have rigor here, estimate 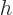 in terms of
in terms of 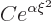 where
where 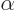 is a number slightly less than one, plus a polynomial.
That is enough to show unacceptability of such solutions.)
is a number slightly less than one, plus a polynomial.
That is enough to show unacceptability of such solutions.)
What are the options for acceptable solutions? The only possibility
is that the power series terminates. There must be a highest power
 , call it
, call it 

 , whose term in the right hand
side is zero
, whose term in the right hand
side is zero
In that case, there is no need for a further 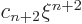 term,
the power series will remain a polynomial of degree
term,
the power series will remain a polynomial of degree  . But
note that all this requires the scaled energy
. But
note that all this requires the scaled energy 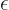 to equal
to equal
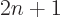 , and the actual energy
, and the actual energy 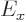 is therefore
is therefore
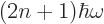
 2. Different choices for the power at which the
series terminates produce different energies and corresponding
eigenfunctions. But they are discrete, since
2. Different choices for the power at which the
series terminates produce different energies and corresponding
eigenfunctions. But they are discrete, since  , as any power
, as any power
 , must be a nonnegative integer.
, must be a nonnegative integer.
With 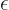 identified as
identified as 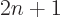 , you can find the ODE for
, you can find the ODE for
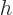 listed in table books, like [41, 29.1], under the
name
listed in table books, like [41, 29.1], under the
name Hermite's differential equation.
They then
identify the polynomial solutions as the so-called “Hermite
polynomials,” except for a normalization factor. To find the
normalization factor, i.e. 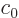 or
or 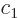 , demand that the total
probability of finding the particle anywhere is one,
, demand that the total
probability of finding the particle anywhere is one,
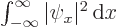
 1. You should be able
to find the value for the appropriate integral in your table book,
like [41, 29.15].
1. You should be able
to find the value for the appropriate integral in your table book,
like [41, 29.15].
Putting it all together, the generic expression for the eigenfunctions
can be found to be:
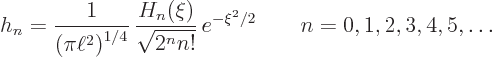 |
(D.4) |
where the details of the Hermite polynomials
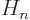 can
be found in table books like [41, pp. 167-168]. They
are readily evaluated on a computer using the “recurrence
relation” you can find there, for as far as computer round-off
error allows (up to
can
be found in table books like [41, pp. 167-168]. They
are readily evaluated on a computer using the “recurrence
relation” you can find there, for as far as computer round-off
error allows (up to  about 70.)
about 70.)
Quantum field theory allows a much neater way to find the
eigenfunctions. It is explained in addendum {A.15.5} or
equivalently in {D.64}.
![]() -
-![]()
![]()
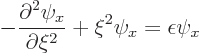
![]()
![]() )
)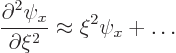
![]()
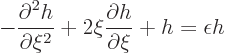
![]()
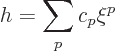
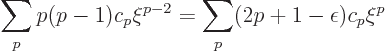
![]()
![]() ,
,![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
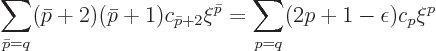
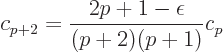
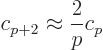
![]() ,
,![]()
![]()
![]() ,
,![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()