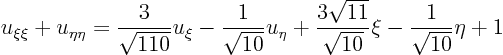|
|
|
|
|
Next: 1.6 Properly Posedness |
|
More powerful simplifications by changing coordinates are possible in 2D.
Assume that in terms of coordinates ![]() and
and ![]() , we have a partial
differential equation:
, we have a partial
differential equation:
For example, for a hyperbolic equation, you may like coordinates ![]() and
and ![]() such that
such that ![]() and
and ![]() are zero. To find out for what
coordinates
are zero. To find out for what
coordinates ![]() and
and ![]() that is the case, expressions for the new
coefficients
that is the case, expressions for the new
coefficients ![]() ,
, ![]() ,
, ![]() and
and ![]() in terms of the new coordinates
are needed. These can be found by writing out the general
transformation formulae from section 1.4.2 for the special
case of two dimensions. You get, {D.4}:
in terms of the new coordinates
are needed. These can be found by writing out the general
transformation formulae from section 1.4.2 for the special
case of two dimensions. You get, {D.4}:
Characteristic coordinates are coordinates so that the the
![]() and
and ![]() derivatives are eliminated. That
leaves only the
derivatives are eliminated. That
leaves only the ![]() derivative, greatly simplifying the
partial differential equation. It reduces to the two-dimensional
canonical form:
derivative, greatly simplifying the
partial differential equation. It reduces to the two-dimensional
canonical form:
| (1.13) |
The first thing is to find out how this may be achieved. In terms of
the coefficients of the transformed equation as discussed above, ![]() and
and ![]() must vanish. The condition
must vanish. The condition ![]() requires, according to
the given formulae:
requires, according to
the given formulae:
To solve the equation for ![]() (
(![]() goes the same way), divide by
goes the same way), divide by
![]() :
:
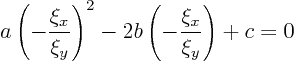
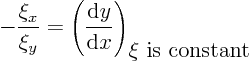
By taking the other sign for the square root, you can get a second
independent coordinate ![]() .
.
Bottom line, to get characteristic coordinates, solve the plus and
minus sign ordinary differential equations above, and equate the
integration constants to ![]() and
and ![]() .
.
A couple of notes:
ExampleQuestion: Use characteristic coordinates to reduce the wave equation in multi-dimensional canonical form
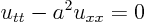
to its equivalent two-dimensional canonical form. Then solve it.Solution:
First find the characteristics by solving the ordinary differential equation given above:
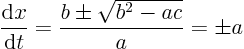
Note that the finalis the wave propagation speed, not the coefficient
in the generic second order equation.
The solution is simple:

whereand
are the integration constants (as well as the characteristic coordinates). So the lines
are one set of characteristic lines, and the lines
are the other set.
Now find the coefficient
. The coefficient
was zero, and the second order derivatives of
and
in the formula for
are also zero, so
is zero too. So the wave equation in characteristic coordinates is
Note that
(1.14) could be divided out, so there is no need to figure out what it is.
The wave equation can now easily be solved. Integration with respect to
gives
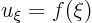
where the integration constantcan be any arbitrary function of
. Integrating with respect to
gives the final solution:
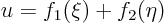
Hereis an antiderivative of
, so it is arbitrary just like
. The additional integration constant
is an arbitrary function of
.
However, you would surely want the solution in terms of the physical coordinates
and
, rather than the mathematical characteristic coordinates. So substitute for
and
using the obtained equations for the characteristics. That gives the final solution:
(1.15) That is the general solution of the wave equation. In order to solve a particular problem, you will still need to figure out what
and
are using whatever the initial and boundary conditions are. One special case, in which the
-range is doubly infinite, will be solved in detail later.
ExampleQuestion: Find and sketch the characteristics of the equation
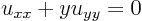
Solution:
Figure out the coefficients in the the characteristic equation by looking at the partial differential equation:

Note that there are only characteristics for negative. For positive
the equation is elliptic. And for zero
there will only be one direction for the characteristics, horizontal.
Use separation of variables to solve. In other words, take the
factors to one side and the
-factors to the other side:
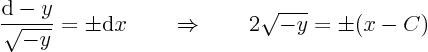
Squaring both sides to get rid of the square root gives

These are parabolae.
ExampleQuestion: Reduce the equation
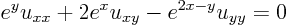
to two-dimensional canonical form.Solution:
Two-dimensional canonical form means characteristic form. Find the ordinary differential equation for the characteristics:

Solve it using separation of variables:
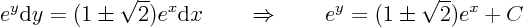
The integration constants are the new coordinates:

Work out the partial differential equation in these coordinates using the formulae given at the start of this section:
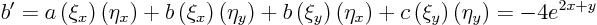
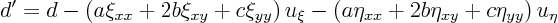
so
![\begin{displaymath}
d' = - \left[(1+\sqrt2)e^{x+y}+ e^{2x}\right] u_\xi
- \left[(1-\sqrt2)e^{x+y}+ e^{2x}\right] u_\eta
\end{displaymath}](img321.gif)
The partial differential equation becomes
![\begin{displaymath}
8 e^{x+y} u_{\xi\eta} =
\left[(1+\sqrt2)e^y+ e^x\right] u_\xi
\left[(1-\sqrt2)e^y+ e^x\right] u_\eta
\end{displaymath}](img322.gif)
Get rid of
and
completely using the equations for the characteristics:
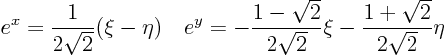
The resulting partial differential equation is
![\begin{displaymath}
(\xi -\eta)[(1-\sqrt2)\xi + (1+\sqrt2)\eta]u_{\xi\eta}
= (1+\sqrt2)\eta u_\xi + (1-\sqrt2)\xi u_\eta
\end{displaymath}](img324.gif)
It does not look easily solvable.
ExampleQuestion: Find the characteristic coordinates of the equation
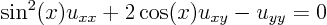
Solution:
Find the ordinary differential equation for the characteristics:

Solve it:
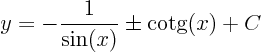
The characteristic coordinates are the integration constants:
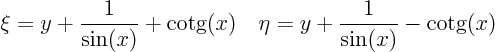
It does not like the partial differential is going to be very simple.
In the parabolic case there is only one equation for the
characteristics because the discriminant ![]() is zero:
is zero:
You will need to take the other coordinate something else, say
![]() . You want to take something simple, but it should be
independent of the other coordinate.
. You want to take something simple, but it should be
independent of the other coordinate.
The partial differential equations then simplifies to the
two-dimensional canonical form
| (1.16) |
You may be surprised by that. In choosing ![]() , all we did was make
the coefficient
, all we did was make
the coefficient ![]() zero. We did not explicitly make
zero. We did not explicitly make ![]() zero. But
zero. But
![]() is zero automatically. The reason is that the physical
properties of partial differential equations do not change just
because you use different coordinates. A parabolic equation should
stay parabolic; there are fundamental differences between the physical
behaviors of parabolic, elliptic, and hyperbolic equations. And the
equation above would not be parabolic if
is zero automatically. The reason is that the physical
properties of partial differential equations do not change just
because you use different coordinates. A parabolic equation should
stay parabolic; there are fundamental differences between the physical
behaviors of parabolic, elliptic, and hyperbolic equations. And the
equation above would not be parabolic if ![]() was nonzero.
was nonzero.
ExampleQuestion: Reduce the equation
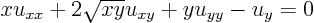
to two-dimensional canonical form.Solution:
Write the equation for the characteristics
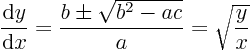
The square root is zero, so the equation is parabolic.Solve the equation and call the integration constant
:
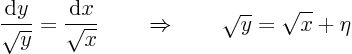
So take the new coordinates as
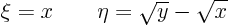
The final partial differential equation then becomes
![\begin{displaymath}
- 4 \xi u_{\xi\xi} =
\left[\frac{1}{\sqrt{\xi}} + \frac{3}{\eta+\sqrt{\xi}}\right] u_{\eta}
\end{displaymath}](img336.gif)
Characteristic lines are solutions to the ordinary differential
equation
Take either sign of the square root. Solve the equation and call the
integration constant, say, ![]() . Then write this integration
constant in the form
. Then write this integration
constant in the form
| (1.17) |
Using ![]() and
and ![]() as the new coordinates, it turns out that the
partial differential equation takes the two-dimensional canonical form:
as the new coordinates, it turns out that the
partial differential equation takes the two-dimensional canonical form:
| (1.18) |
There are significant limitations on this procedure, however, {D.5}
ExampleQuestion: Reduce the equation
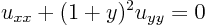
to two-dimensional canonical form.Solution:
Write the equation for the characteristics

This is complex, so the equation is elliptic.Solve using separation of variables

The new coordinates can therefore be chosen as
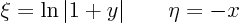
In terms of these coordinates, the equation becomes
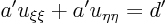
The new partial differential equation becomes

Convert the equation
Using rotation and stretching of the coordinates you would get