| Partial Differential Equations 0.15 alpha |
|
© Leon van Dommelen |
|
D.5 2D elliptical transformation
To bring two-dimensional elliptical equations in the two-dimensional
canonical form, you need to solve, say, the ordinary differential
equation
Note now that even if you take 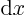 to be real,
to be real, 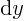 will be
complex. And that means that you need to know what happens to the
coefficients
will be
complex. And that means that you need to know what happens to the
coefficients 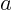 ,
, 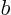 , and
, and 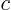 when you depart the real
when you depart the real 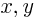 -plane
into the complex domain. That may be fine if you know the
coefficients analytically, but otherwise it is a problem.
-plane
into the complex domain. That may be fine if you know the
coefficients analytically, but otherwise it is a problem.
Assuming that you can solve the system, call the integration constant
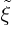 . Assuming that it is a differentiable function of
. Assuming that it is a differentiable function of 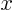 and
and
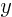 , it will satisfy
, it will satisfy
Now set
If you plug that in the equation above and multiply out, you get
Now within the square brackets above, you find the generic expressions
for the coefficients 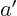 ,
, 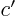 and
and 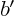 , respectively, of the
transformed partial diffential equation. For a complex number to be
zero, both its real and its imaginary part must be zero. It follows
that
, respectively, of the
transformed partial diffential equation. For a complex number to be
zero, both its real and its imaginary part must be zero. It follows
that 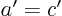 and that
and that 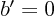 .
.
![]() to be real,
to be real, ![]() will be
complex. And that means that you need to know what happens to the
coefficients
will be
complex. And that means that you need to know what happens to the
coefficients ![]() ,
, ![]() , and
, and ![]() when you depart the real
when you depart the real ![]() -plane
into the complex domain. That may be fine if you know the
coefficients analytically, but otherwise it is a problem.
-plane
into the complex domain. That may be fine if you know the
coefficients analytically, but otherwise it is a problem.
![]() . Assuming that it is a differentiable function of
. Assuming that it is a differentiable function of ![]() and
and
![]() , it will satisfy
, it will satisfy
![\begin{eqnarray*}
&& [a (\xi_x)^2 + 2 b \xi_x\xi_y + c(\xi_y)^2] -
[a (\eta_...
... \xi_x\eta_x + b \xi_x\eta_y + b \xi_y\eta_x + c\xi_y\eta_y] =0
\end{eqnarray*}](img1564.gif)