| Partial Differential Equations 0.15 alpha |
|
© Leon van Dommelen |
|
D.4 2D coordinate transformation derivation
This note gives a more detailed description where the
expressions (1.12) for the coefficients 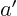 ,
, 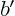 ,
, 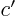 and
and 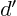 comes from.
comes from.
In terms of the notations for the general case, you have
and
The introduction noted that the new coefficients can be found from
As an example, let’s find the value for 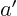 . In terms of the
notations in the general case,
. In terms of the
notations in the general case, 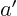 is the 1,1 element of matrix
is the 1,1 element of matrix 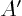 :
:
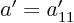 . To get
. To get 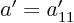 , put
, put 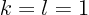 in
in
That turns 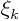 and
and 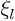 into
into 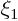 , or
, or 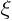 for short:
for short:
If we write out the four terms of the double sum explicitly,
that becomes:
Now note that by definition 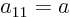 ,
,
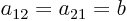 ,
, 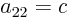 ,
,
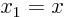 , and
, and 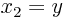 , and you get the expression for
, and you get the expression for 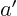 claimed:
claimed:
The expressions for 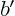 ,
, 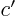 and
and 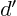 may be verified
similarly.
may be verified
similarly.
![]() ,
, ![]() ,
, ![]() and
and ![]() comes from.
comes from.

![]() . In terms of the
notations in the general case,
. In terms of the
notations in the general case, ![]() is the 1,1 element of matrix
is the 1,1 element of matrix ![]() :
:
![]() . To get
. To get ![]() , put
, put ![]() in
in
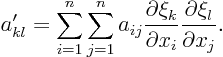
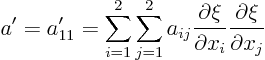
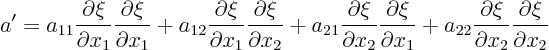
![]() ,
, ![]() and
and ![]() may be verified
similarly.
may be verified
similarly.