|
|
|
|
Skip to: 1.6 Properly Posedness |
|
Convert the equation
Using rotation and stretching of the coordinates you would get
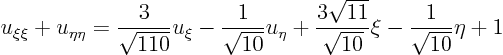
Answer:
You get
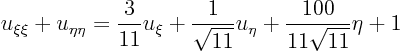
You do not necessarily get the same result. If you rotate the coordinate system, the Laplacian stays the same, but the right hand side changes.