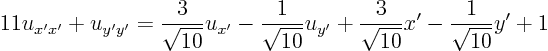|
|
|
|
|
Next: 1.5 Two-Dimensional Coordinate Transforms |
|
Changes of coordinates are a primary way to understand, simplify, and sometimes even solve, partial differential equations.
It is possible to simplify many partial differential equation problems by using coordinate systems that are special to the problem:
Assume the purpose is to address a problem in an ![]() -dimensional
space. The coordinates in this space form a vector
-dimensional
space. The coordinates in this space form a vector
The idea is now to switch to some new set of independent coordinates
The change of coordinates is characterized by Jacobian matrices
that have coefficients
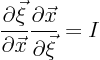
The purpose is now to simplify second order quasi-linear partial
differential equations using coordinate transforms. As noted in the
previous section, second order quasi-linear equations are of the form
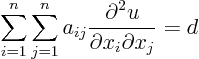
Of course, before you can do anything clever like that, you have to
first know what happens to the partial differential equation when the
coordinates are changed. It turns out that the form of the
equation remains the same in the new coordinates:
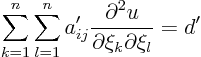
The expression for the new matrix ![]() can be written in either matrix
notation or index notation. It is
can be written in either matrix
notation or index notation. It is
Using equations (1.7) and (1.8) above, you
can figure out what the new matrix and right hand side are. However,
that may not yet be enough to fully transform the problem to the new
coordinates. Recall that the coefficients ![]() and
and ![]() might
involve first order derivatives with respect to
might
involve first order derivatives with respect to
![]() .
These derivatives must be converted to derivatives with respect to
.
These derivatives must be converted to derivatives with respect to
![]() . To do that, use:
. To do that, use:
That may still not be enough, because the resulting equation will
probably still contain
![]() themselves. You will also
need to express these in terms of
themselves. You will also
need to express these in terms of
![]() to get the
final partial differential equation completely in terms of the new
coordinates.
to get the
final partial differential equation completely in terms of the new
coordinates.
But that is it. You are now done. At least with the partial differential equation. There might also be boundary and/or initial conditions to invert. That can be done in a similar way, but we will skip it here.
One additional point should be made. If you follow the procedure
exactly as outlined above, you will have to express
![]() in terms of
in terms of
![]() , and differentiate
these expressions. You will also need to express
, and differentiate
these expressions. You will also need to express
![]() in
terms of
in
terms of
![]() to get rid of
to get rid of
![]() in the
equations. But if you are, say, switching from Cartesian to sperical
coordinates, the expressions for the spherical coordinates in terms of
the Cartesian ones are awkward. You would much rather just deal with
the expressions of the Cartesian coordinates in terms of the spherical
ones.
in the
equations. But if you are, say, switching from Cartesian to sperical
coordinates, the expressions for the spherical coordinates in terms of
the Cartesian ones are awkward. You would much rather just deal with
the expressions of the Cartesian coordinates in terms of the spherical
ones.
Just dealing with
![]() in terms of
in terms of
![]() can be done with a bit of manipulation. To get the Jacobian matrix
that you want, evaluate it as the inverse of the other one:
can be done with a bit of manipulation. To get the Jacobian matrix
that you want, evaluate it as the inverse of the other one:
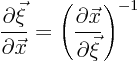
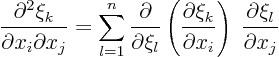
Derivation {D.3} gives the derivation of the various formulae above.
The purpose of this section is to simplify second order partial differential equations by rotating the coordinate system over a suitable angle. It should be noted straight away that this procedure tends to be largely limited to constant coefficient linear equations.
If you simply rotate the coordinate system, Cartesian coordinates stay
Cartesian. For example, suppose that the original coordinates are
Cartesian coordinates ![]() ,
, ![]() , and
, and ![]() , and that the unit vectors
along the axes are
, and that the unit vectors
along the axes are ![]() ,
, ![]() , and
, and ![]() . Then the new
coordinates, call them
. Then the new
coordinates, call them ![]() ,
, ![]() , and
, and ![]() , are also Cartesian, but
with different unit vectors
, are also Cartesian, but
with different unit vectors ![]() ,
, ![]() , and
, and ![]() .
.
In any number of dimensions, the original coordinates will be
indicated by
![]() and the rotated coordinates
and the rotated coordinates
![]() . (Using
. (Using ![]() instead of
instead of ![]() like in the previous
subsection seems more appropriate for coordinates that are merely
rotated.) The axial unit vectors of the original coordinate system
will be called
like in the previous
subsection seems more appropriate for coordinates that are merely
rotated.) The axial unit vectors of the original coordinate system
will be called
![]() , and those of the rotated
coordinates
, and those of the rotated
coordinates
![]() .
.
The original partial differential equation takes the form
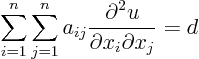
The partial differential equation in the rotated coordinates takes a
similar form as in the original system:
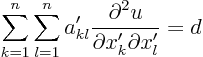
For the right rotation of the coordinate system, the coefficients
![]() will be much simpler than the original coefficients
will be much simpler than the original coefficients
![]() . In particular, all coefficients
. In particular, all coefficients ![]() with
with ![]() not
equal to
not
equal to ![]() will then be zero.
will then be zero.
The question is now how to find this right rotation of coordinates.
In other words, the question is how to choose the new unit vectors
![]() so that all coefficients
so that all coefficients ![]() with
with ![]() not equal to
not equal to ![]() are zero.
are zero.
The answer is simple. The vectors
![]() must be
the eigenvectors of matrix
must be
the eigenvectors of matrix ![]() . Of course, make sure that you
normalize the eigenvectors of matrix
. Of course, make sure that you
normalize the eigenvectors of matrix ![]() to length 1 before you take
them to be
to length 1 before you take
them to be
![]() . And if there is ambiguity in
their direction, (which happens if two or more eigenvalues are equal),
make sure that the eigenvectors you choose are mutually orthogonal.
(Since
. And if there is ambiguity in
their direction, (which happens if two or more eigenvalues are equal),
make sure that the eigenvectors you choose are mutually orthogonal.
(Since ![]() is a symmetric matrix, these requirements can always be
met.)
is a symmetric matrix, these requirements can always be
met.)
There is really no need to compute the new matrix ![]() from equation
(1.7) of the previous subsection. If you do everything
right,
from equation
(1.7) of the previous subsection. If you do everything
right, ![]() will be zero if
will be zero if ![]() and
and ![]() are not equal. And a
coefficient of the form
are not equal. And a
coefficient of the form ![]() will be
will be ![]() , the eigenvalue
number
, the eigenvalue
number ![]() of matrix
of matrix ![]() . (That is regardless of whatever numbering
system you selected. But number eigenvalues and corresponding
eigenvectors the same way.)
. (That is regardless of whatever numbering
system you selected. But number eigenvalues and corresponding
eigenvectors the same way.)
In short, the new matrix of coeficients will be a diagonal one, of the
form
The conversion formulae between the coordinates are:
The second formula in (1.11) implies that the right hand side
![]() is the same in the transformed equation as in the original one:
is the same in the transformed equation as in the original one:
![]() are linear in
are linear in
![]() , so their second
order derivatives in (1.8) are zero.
, so their second
order derivatives in (1.8) are zero.
You will need the first formula in (1.11), in terms of its
components, to get rid of any coordinates
![]() in the
right hand side
in the
right hand side ![]() in favor of
in favor of
![]() . Also, if
. Also, if ![]() contains derivatives with respect to the unknowns
contains derivatives with respect to the unknowns
![]() ,
you will need to convert those using (1.9) of the
previous subsection. To get the derivatives
,
you will need to convert those using (1.9) of the
previous subsection. To get the derivatives
![]() with
respect to
with
respect to
![]() while doing so, write out the second
formula in (1.11) in terms of its components.
while doing so, write out the second
formula in (1.11) in terms of its components.
Some books, like [1], do not bother to
normalize the eigenvectors to length one. In that case the coordinate
transformation is not just a rotation, but also a stretching of the
coordinate system. The matrix ![]() is still diagonal, but the values
on the main diagonal are no longer the eigenvalues of
is still diagonal, but the values
on the main diagonal are no longer the eigenvalues of ![]() . Also, it
becomes messier to find the old coordinates in terms of the new ones.
Using orthonormal rather than just orthogonal eigenvectors is
recommended.
. Also, it
becomes messier to find the old coordinates in terms of the new ones.
Using orthonormal rather than just orthogonal eigenvectors is
recommended.
ExampleQuestion: Classify the equation
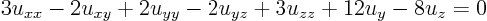
and put it in canonical form.Solution:
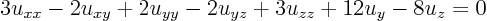
Identify the matrix:
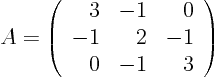
To find the new coordinates (transformation matrix), find the eigenvalues and eigenvectors of
:
The eigenvalues are the roots of
:
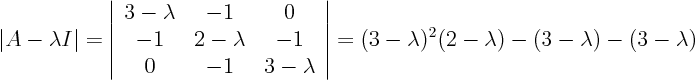
Hence,
,
.
The eigenvectors are solutions of
that are normalized to length one. For
, writing matrix
and applying Gaussian elimination on it produces
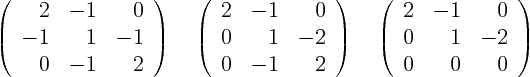
which gives the normalized eigenvector
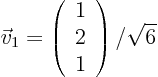
For
,
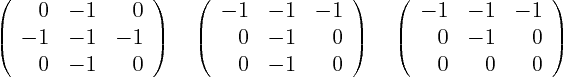
which gives the normalized eigenvector
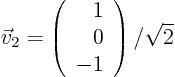
For
,
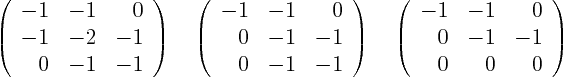
which gives the normalized eigenvector
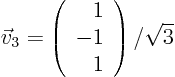
The new equation is:
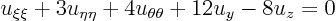
However, that still contains the old coordinates in the first order terms. Use the transformation formulae and total differentials to convert the first order derivatives:
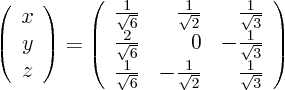
and its inverse
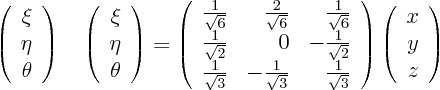
The partial derivatives of
with respect to
can be read off from the final matrix. So
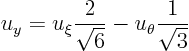
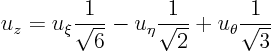
Hence in the rotated coordinate system, the partial differential equation is:
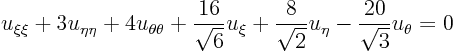
Simplify the partial differential equation
The previous subsection showed how partial differential equations can be simplified by rotating the coordinate system. Using this procedure it is possible to understand why second order partial differential equations are classified as described in section 1.3.2.
Rotation of the coordinate system reduces a partial differential
equation of the form
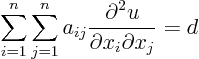
That immediately explains why only the eigenvalues of matrix ![]() are
of importance for the classification. Rotating the mathematical
coordinate system obviously does not make any difference for the
physical nature of the solutions. And in the rotated coordinates, all
that is left of matrix
are
of importance for the classification. Rotating the mathematical
coordinate system obviously does not make any difference for the
physical nature of the solutions. And in the rotated coordinates, all
that is left of matrix ![]() are its eigenvalues.
are its eigenvalues.
The next question is why the classification only uses the signs of the eigenvalues, not their magnitudes. The reason is that the magnitude can be scaled away by stretching the coordinates. That is demonstrated in the next example.
ExampleQuestion: The previous example reduced the elliptic partial differential equation
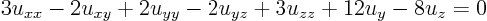
to the form
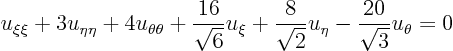
Reduce this equation further until it becomes as closely equal to the Laplace equation as possible.Solution:
The first step is to make the coefficients of the second order derivatives equal in magnitude. That can be done by stretching the coordinates. If
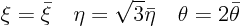
then
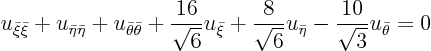
Note that all that is left in the second order derivative terms is the sign of the eigenvalues.
You can get rid of the first order derivatives by changing to a new independent variable
. To do so, set
. Plug this into the differential equation above and differentiate out the product. Then choose
,
, and
so that the first derivatives drop out. You will find that you need:
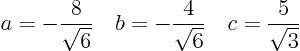
Then the remaining equation turns out to be:
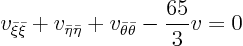
It is not exactly the Laplace equation because of the final term. But the final term does not even involve a first order derivative. It makes very little difference for short-scale phenomena. And short scale phenomena (such as singularities) are the most important for the qualitative behavior of the partial differential equation.
As this example shows, the values of the nonzero eigenvalues can be normalized to 1 by stretching coordinates. However, the sign of the eigenvalues cannot be changed. And neither can you change a zero eigenvalue into a nonzero one, or vice-versa, by stretching coordinates.
You might wonder why all this also applies to partial differential
equations that have variable coefficients ![]() and
and ![]() . Actually,
what
. Actually,
what ![]() is does not make much of a difference. But generally
speaking, rotation of the coordinate system only works if the
coefficients
is does not make much of a difference. But generally
speaking, rotation of the coordinate system only works if the
coefficients ![]() are constant. If they depend on position, the
eigenvectors
are constant. If they depend on position, the
eigenvectors
![]() at every point can still be
found. So it might seem logical to try to find the new coordinates
at every point can still be
found. So it might seem logical to try to find the new coordinates
![]() from solving
from solving
![]() . But
the problem is that that are
. But
the problem is that that are ![]() equations for only
equations for only ![]() unknown
coordinates. If the unit vectors are not constant, these equations
normally mutually conflict and cannot be solved.
unknown
coordinates. If the unit vectors are not constant, these equations
normally mutually conflict and cannot be solved.
The best that can normally be done for arbitrary ![]() is to select a
single point that you are interested in. Then rotate the coordinate
system to diagonalize the partial differential equation at that one
point. In that case,
is to select a
single point that you are interested in. Then rotate the coordinate
system to diagonalize the partial differential equation at that one
point. In that case, ![]() is diagonal near the considered point. And
that is enough to classify the equation at that point. For, the most
important feature that the classification scheme tries to capture is
what happens to short scale phenomena. Short scale phenomona will
“see” the locally diagonal equation. So the
classification scheme continues to work.
is diagonal near the considered point. And
that is enough to classify the equation at that point. For, the most
important feature that the classification scheme tries to capture is
what happens to short scale phenomena. Short scale phenomona will
“see” the locally diagonal equation. So the
classification scheme continues to work.
Convert the equation