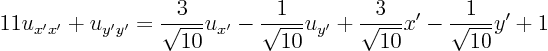| Partial Differential Equations Solution Manual |
|
© Leon van Dommelen |
|
Question:
Simplify the partial differential equation
by rotating the coordinate system. Classify the equation. Draw the original and rotated coordinate system and identify the angle of rotation.
Answer:
Identify the matrix 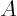 . Find the eigenvalues and orthonormal eigenvectors. You find
. Find the eigenvalues and orthonormal eigenvectors. You find
The eigenvalues are of the same sign, so it is elliptic.
You then find the relation between the coordinates to be
So using the conversion rule for the first derivative 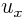 , the PDE becomes
, the PDE becomes
![]() . Find the eigenvalues and orthonormal eigenvectors. You find
. Find the eigenvalues and orthonormal eigenvectors. You find
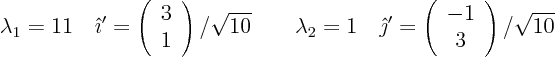
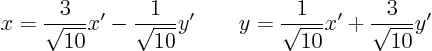
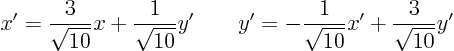
![]() , the PDE becomes
, the PDE becomes