1.6 Properly Posedness

Properly posedness is really quite unique to partial differential equations. Ordinary differential equations can be hard to solve if they involve very different time scales. For example, that is an issue in many chemical reactions.

But for partial differential equations, “hard to solve” becomes “impossible to solve.” That happens even for apparently very simple linear partial differential equations with constant coefficients.

This section has a look at some of the issues involved.

1.6.1 The conditions for properly posedness

In words, a properly posed problem in partial differential equations can be described as follows: it is a problem that has a unique solution that is physically reasonable.

Phrased more mathematically, a problem is properly posed if:

1. A solution exists. Of course. Note it can be much harder to show that a decent solution exists for partial differential equations than for ordinary differential equations. For example, it has not yet been achieved for the unsteady three-dimensional Navier-Stokes equations of viscous flows of simple fluids.
2. The solution is unique. Of course.
3. Small changes in the data produce correspondingly small changes in the solution. The “data” are here such things as the initial or boundary conditions or an inhomogeneous term in the equation.

Requirement 3 above is the one that makes the solution physically reasonable. Physically, nothing is exactly known. There are always some errors in the data, however accurate they may be. If these negligible errors can produce a significant change in the solution, then all bets are off that the solution obtained is the right one.

You may wonder what “correspondingly small” in condition 3 really means. The true answer is that it varies. However, generally it is taken to mean that changes in the solution are no more than proportional to the changes in the data that cause these changes. And there must be some overall upper bound to the constant of proportionality that is independent of the details of the change in data.

That still requires that suitable measures of the magnitude of the changes in data and solution are defined. That however is beyond this discussion.

One thing should be emphasized. It is not partial differential equations that are properly or improperly posed. It is problems that are properly or improperly posed. Before you know what boundary and initial conditions are specified for your partial differential equation, you cannot say anything meaningful about properly posedness.

The following subsections give a few typical examples of how improperly posed problems arise. It illustrates that if you try to solve some partial differential equation numerically, you better know what sort of equation it is. Or you can get into major problems.

1.6.1 Review Questions

1

Show that the Dirichlet boundary-value problem for the Poisson equation on a finite domain,

$$\nabla^2 u = f \quad\mbox{on}\quad\Omega\qquad u = g \quad\mbox{on}\quad\delta\Omega$$

has unique solutions. Assuming that there is a solution, there is only one.

Solution ppc-a

2

Assuming that the Dirichlet boundary-value problem for the Laplace equation on a finite domain,

$$\nabla^2 u = 0 \quad\mbox{on}\quad\Omega\qquad u = f \quad\mbox{on}\quad\delta\Omega$$

is solvable, show that it depends continuously on the data.

Solution ppc-b

3

Repeat the previous two questions for the Dirichlet initial / boundary value problem for the heat equation,

$$u_t = \kappa\nabla^2 u \quad\mbox{on}\quad\Omega\qquad u = f... ...\mbox{on}\quad\delta\Omega\qquad u = g \quad\mbox{at}\quad t=0$$

Solution ppc-c

1.6.2 An improperly posed parabolic problem

This subsection will discuss an improperly posed problem involving the heat equation. Recall that the heat equation is an example of a parabolic equation.

Consider first a very standard properly posed problem for the heat equation. The problem is heat conduction in a bar. The unknown is the temperature. The ends of the bar are kept at zero temperature.

The below figure shows some computed temperature profiles in a bar at various times.

At the initial time $t=0$ the initial condition was assumed to be piecewise linear. There is then a singularity, a kink, at the center of the bar. A kink corresponds to a jump in the derivative. But the heat equation smooths away singularities. At any later time, even as small as 0.02 in the nondimensional units used in this problem, the temperature profile is perfectly smooth, with all derivatives continuous.

This problem was properly posed. Improperly posedness arises for the “backward heat equation”. Physically the backward heat equation is the heat equation solved backwards in time. Mathematically, the backward heat equation takes the form

$$u_\tau = - \kappa u_{xx}$$

where the new independent variable $\tau$ increases when the time $t$ decreases.

Note that the backward heat equation is equivalent to solving the normal heat equation forwards in time, but with a negative heat conduction coefficient. A negative heat conduction coefficient violates the second law of thermodynamics, so it is not really surprising that you get into trouble with the mathematics.

Suppose that you take the temperature profile $u$ at time $t=1$ in the figure above as the initial condition for the backward heat equation. Then you compute the solution of the backward heat equation up to $\tau=1$. That should give you back the singular temperature profile at time zero. And it will, if you manage to do it exactly. The backward heat equation has a unique solution for the chosen initial condition in the interval from $\tau=0$ to $\tau=1$.

But now suppose that you use the singular profile $u$ at time zero as the initial condition for the backward heat equation. Then you try again to compute the solution of the backward heat equation up to $\tau=1$. It will not work. You will not be able to find a solution for any value of $\tau$ greater than zero. The reason is easy to understand. Suppose that you did find a solution $u$ at $\tau=1$. Physically that would be a temperature distribution in the bar at time $t=-1$. But if a temperature distribution at time $t=-1$ existed, even a singular one, then the temperature distribution would be smooth for all times greater than $-1$. The heat equation smooths away singularities. But the solution at times greater than $-1$ is not nonsingular, because we know it is singular at time zero. So a solution at time $-1$ can simply not exist.

Now let’s return to the problem that did have a unique solution. That was when we started the backward heat equation solution from the smooth temperature profile at $t=1$. There is still a major physical problem with the solution. Physically, (and also in typical numerical solutions), the initial profile will not be exact to infinitely many digits at all locations. There will always some error. Suppose in particular that the actual profile has a very slight kink. It can be so tiny that you cannot see the error in the profile under a microscope if you plot it versus the exact one. But if there is a kink, there is no longer a solution to the backward wave equation. There cannot be a solution at earlier times if there is a singularity, however invisible the kink may be.

In physics your data, here being the temperature profile, are never truly exact. So you have no way of saying which one is the right answer, the unique solution or a complete lack of any solution at all. If the data have any imperfection, it is the latter.

The bottom line is that even though the backward heat equation can have unique solutions for some problems, these solutions are only meaningful if you have a problem that is mathematically exact. So the initial/boundary-value problem for the backward heat equation is improperly posed. Even though it may have unique solutions.

The pure initial-value problem is similarly improperly posed.

1.6.3 An improperly posed elliptic problem

A typical improperly posed problem for the Laplace equation is shown in figure 1.4. Physically, it might correspond to heat conduction in a rectangular plate. For mathematical convenience, the horizontal size of the plate has been rescaled to length $\pi$.

Figure 1.4: An improperly posed Laplace problem.

What is wrong in figure 1.4 is that both the temperature and the heat flow are specified at the lower boundary $y=0$. That is wrong because the Laplace equation needs exactly one boundary condition at each point of the boundary, not two. It is also wrong that no boundary condition at all is given on the top boundary $y=h$.

Mathematically speaking, you might say that figure 1.4 is an initial / boundary-value problem for the Laplace equation, with $y$ playing the part of time. And initial / boundary-value problems for the Laplace equation are not allowed. Note however that figure 1.4 would be perfectly fine if the partial differential equation was $u_{yy}=u_{xx}$ instead of $u_{yy}=-u_{xx}$. That would be a wave equation with a unit wave velocity, and initial/boundary-value problems are just what you want for wave equations. In short, a single sign in the partial differential equation makes all the difference.

The primary problem with initial/boundary-value problems for the Laplace equation is that they do not meet the third requirement for properly posedness. The effect of small changes in the data on the solution can be much larger than the small changes. For the example figure 1.4, that should be taken to mean that the solution $u$ inside the plate can be much larger than the given value $f(x)$ of $u$ at the lower boundary.

That can be seen as follows. Consider the following type of solution:

$$u(x,y) = \sin(nx)\cosh(ny)$$

where $n$ is a natural number, one of 1, 2, 3, ...For a homework, you can verify that the above is a perfectly valid solution to the problem figure 1.4 when $f(x)=\sin(nx)$. It also happens to be unique.

Now note that the “data”, the values of $f(x)$, are no greater than 1 in magnitude. On the other hand, in the interior of the plate, $u$ can reach values up to $\cosh(nh)$. For any given value of $n$ that is a finite number. But there is no universal bound to it. You can make $\cosh(nh)$ as large as you want by just taking $n$ large enough. The value of $\cosh(1)$ is only about 1.5, but $\cosh(100)$ is already about $10^{43}$. In short, the size of $u$ can exceed the size of $f$ by any arbitrarily large factor.

1.6.3 Review Questions

1

Show that the given solution

$$u(x,y) = \sin(nx)\cosh(ny)$$

for natural $n$ does indeed satisfisfy the Laplace equation

$$u_{yy}+u_{xx}=0$$

and the boundary conditions

$$u(x,0)=\sin(x)\quad u_y(x,0)=0 \quad u(0,y)=0 \quad u(\pi ,y)=0$$

Solution ppe-a

2

Check the separation of variables solution to the above problem,

$$u(x,y) = \sum_{n=1}^\infty f_n \sin(nx) \cosh(ny)$$

Here the “Fourier coefficients” $f_n$ are chosen so that they satisfy

$$f(x) = \sum_{n=1}^\infty f_n \sin(nx)$$

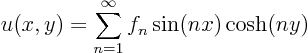
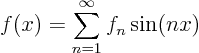
Can you immediately see that this separation of variables solution is probably no good?

Solution ppe-b

3

Plot the separation of variables solution of the previous question for an example. Assume that the given boundary condition is a triangular profile:

$$f(x)=x \quad\mbox{if}\quad x\le{\textstyle\frac{1}{2}} \pi\q... ...(x)=\pi -x \quad\mbox{if}\quad x\ge{\textstyle\frac{1}{2}} \pi$$

Comment on whether a solution $u$ exists at $y=0$ and for $y>0$.

This example should illustrate that typical improperly posed problems might have solutions if the data are perfectly smooth and their Taylor series have finite radii of convergence. But if there is a singularity, like the kink in the triangular profile, all bets are off.

You might know that if you talk about instability of ordinary differential equations, you wonder about what happens to the solution for infinite time. But in this problem you do not let the “time” coordinate $y$ go to infinity. The problem is not large $y$, but large “wave number” $n$. The large wave number problem is really unique to partial differential equations. (If you had a system of infinitely many ordinary differential equations, you might also run into it.)

Solution ppe-c

4

Continuing the previous question, show analytically that for the supposed solution

$$u(x,y) = \sum_{n=1}^\infty\frac{4}{\pi n^2} \sin\left(n{\textstyle\frac{1}{2}}\pi\right) \sin(nx) \cosh(ny)$$

the sum does not converge for any $x$ if $y>0$.

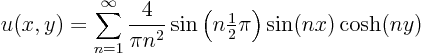
Also show analytically that at the halfway point $x=\frac 12\pi$, the values that you get while summing increase monotonically to infinity.

Solution ppe-d

5

Show that the Laplace equation

$$\nabla^2 u = 0 \qquad\mbox{inside}\qquad\Omega$$

with the Neumann boundary condition

$$\frac{\partial u}{\partial n} = 1 \qquad\mbox{on}\qquad\delta\Omega$$

has no solution. That makes it an improperly posed problem.

Explain the lack of solution in physical terms. To do so, consider this a steady heat conduction problem, with $u$ the temperature, and the gradient of $u$ the scaled heat flux.

Generalize the derivation to determine the requirement that

$$\nabla^2 u = f \qquad\mbox{inside}\qquad\Omega$$

with the Neumann boundary condition

$$\frac{\partial u}{\partial n} = g \qquad\mbox{on}\qquad\delta\Omega$$

has a solution.

Solution ppe-e

6

Show that if the Poisson equation

$$\nabla^2 u = f \qquad\mbox{inside}\qquad\Omega$$

with the Neumann boundary condition

$$\frac{\partial u}{\partial n} = g \qquad\mbox{on}\qquad\delta\Omega$$

has a solution, it is not unique.

Solution ppe-f

1.6.4 Improperly posed hyperbolic problems

A typical improperly posed problem for the wave equation is shown in figure 1.5. Physically, it might correspond to transverse vibrations of a string over a finite time interval. For mathematical convenience, the length of the string has been rescaled to length $\pi$. Also, the time has been rescaled to eliminate the wave speed $c$ from the wave equation. The scaled final time has been written as $T\pi$, again for mathematical convenience, but the value of $T$ can be anything.

Figure 1.5: An improperly posed wave equation problem.

What is wrong in figure 1.5 is that instead of specifying the initial position and velocity of the string, the initial and final position of the string are given. That is wrong because the wave equation is an evolution equation. It requires initial conditions, not final conditions.

Mathematically speaking, you might say that figure 1.5 is an boundary-value problem for the wave equation, with $t$ playing the part of a spatial coordinate. Boundary-value problems for the wave equation are not allowed. Note however that figure 1.5 would be perfectly fine if the partial differential equation was $u_{tt}+u_{xx}=0$ instead of $u_{tt}-u_{xx}=0$. That would be the Laplace equation, and boundary-value problems are just what you want for the Laplace equation. In short, a single sign in the partial differential equation makes all the difference.

The given problem has special solutions of the form

$$u =\sin(nx)\sin(nt)$$

where $n$ is an integer. For such a solution

$$f(x)=\sin(n T\pi)\sin(nx)$$

The reason for the fact that figure 1.5 produces an improperly posed problem depends on the value of $T$. Consider first the possibility that $T$ is a rational number. A rational number is a number that can be written as

$$T=\frac{m_1}{m_2}$$

where $m_1$ and $m_2$ are integers.

For such a rational $T$, the solution to the problem figure 1.5 is not unique. The quickest way to see that is to take the function $f(x)$ in the given problem zero. Then one solution to the problem is obviously $u=0$. So any nonzero solution means that the solution is not unique. And you get a nonzero solution by taking $n=m_2$ or any whole multiple of $m_2$ in the special solutions given above.

Since the solution is not unique, the problem violates the second condition for properly posed problems.

Not all numbers are rational numbers, however. In fact, in some sense there are infinitely many more irrational numbers than rational ones. One simple example is $\sqrt{2}$. Irrational numbers can however be approximated to arbitrary accuracy by rational ones. For example, consider $\sqrt{2}$ to 10 digits accuracy:

$$\sqrt{2} \approx 1.414213562 = \frac{1414213562}{1000000000}$$

The same way, any irrational $T$ value is arbitrarily close to rational ones, and for rational ones the problem figure 1.5 is improperly posed. So surely you would not expect the boundary value problem to be properly posed for an irrational $T$ value. What happens in this case is that the criterion 3 for properly posedness is violated. Consider again the special solutions above. In the interior of the rectangle, the solution $u =\sin(nx)\sin(nt)$ clearly has magnitude 1. (Or something comparable to 1, if you want to use an average magnitude as measure.) The data $f(x)=\sin(nT\pi)\sin(nx)$ however have magnitude $\sin(nT\pi)$. So, if you can find values for $n$ that make $\sin(nT\pi)$ arbitrarily small, you have shown that criterion 3 is violated. The magnitude of $u$ would be much larger than the magnitude of $f$. Try solving the corresponding homework question only if you are really good in math.

Finally, you might argue that initial/boundary-value problems are not really required for the wave equation. Since $x$ appears in the wave equation exactly like $t$ does, surely you should be able to provide two “initial conditions” at $x=0$ instead of $t=0$. And provide one “boundary condition” at $t=0$ and one “boundary condition” at $t=T\pi$. Physically that is not an initial/boundary-value problem; it might be called an initial/final/single-doubled-boundary-value problem.

You have a good point there. The stated problem is indeed properly posed, as you say. However, that trick only works in one-spatial dimension. For the wave equation in two spatial dimensions,

$$u_{tt} = c^2 \left(u_{xx} + u_{yy}\right)$$

trying to specify “initial conditions” at $x=0$ will produce an improperly posed problem. To see why, simply consider solutions that are independent of time. For such solutions, initial conditions at $x=0$ would produce an initial value problem for the Laplace equation in $x$ and $y$. That is improperly posed.

1.6.4 Review Questions

1

Show that the given solution

$$u(x,y) = \sin(nx)\sin(nt)$$

with $n=m_2$ does indeed satisfisfy the wave equation

$$u_{tt} = u_{xx}$$

and the boundary conditions

$$u(x,0)=0 \quad u(0,t)=0 \quad u(\pi ,t)=0 \quad u(x,\frac{m_1}{m_2}\pi)=0$$

How about twice that solution? Ten times? How about if $n=2m_2$? How about if $n=10m_2$? So how many solutions are there really to this single problem?

Solution pph-a

2

For the brave. Show without peeking at the solution that the problem for irrational $T$ is improperly posed by showing that you can make

$$\sin(nT\pi)$$

arbitrarily large by choosing suitable values of $n$.

Solution pph-b