| Partial Differential Equations Solution Manual |
|
© Leon van Dommelen |
|
Question:
Show that the Dirichlet boundary-value problem for the Poisson equation on a finite domain,
has unique solutions. Assuming that there is a solution, there is only one.
Answer:
Suppose that there are two solutions  and
and  . For nonuniqueness, the difference
. For nonuniqueness, the difference 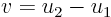 must be nonzero.
must be nonzero.
Show that 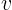 satisfies the Laplace equation by subtracting the Poisson equations satisfied by
satisfies the Laplace equation by subtracting the Poisson equations satisfied by  and
and  . Show that
. Show that 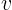 is zero on the boundaries by subtracting the boundary conditions satisfied by
is zero on the boundaries by subtracting the boundary conditions satisfied by  and
and  .
.
Now use the maximum and minimum properties of the Laplace equation to show that 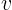 is zero. That means that
is zero. That means that 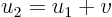 equals
equals  . So the supposed two different solutions are not different.
. So the supposed two different solutions are not different.
![]() and
and ![]() . For nonuniqueness, the difference
. For nonuniqueness, the difference ![]() must be nonzero.
must be nonzero.
![]() satisfies the Laplace equation by subtracting the Poisson equations satisfied by
satisfies the Laplace equation by subtracting the Poisson equations satisfied by ![]() and
and ![]() . Show that
. Show that ![]() is zero on the boundaries by subtracting the boundary conditions satisfied by
is zero on the boundaries by subtracting the boundary conditions satisfied by ![]() and
and ![]() .
.
![]() is zero. That means that
is zero. That means that ![]() equals
equals ![]() . So the supposed two different solutions are not different.
. So the supposed two different solutions are not different.