1.7 Energy methods

Energy methods derive some sort of system “energy” from a partial differential equation. That energy may then be used to derive such things as existence and/or uniqueness of the solution, and whether it depends continuously on the data.

1.7.1 The Poisson equation

Consider the following very general Poisson equation problem:

$$\nabla^2 u = f \quad\mbox{in}\quad \Omega \qquad A u +... ...partial u}{\partial n} = g \quad\mbox{on}\quad \delta\Omega$$

This includes the Laplace equation; just take $f=0$. It includes Dirichlet boundary conditions, (take $B=0$), and Neumann boundary conditions, (take $A=0$).

The objective in this subsection is to show that solutions to this problem are unique as long as $A$ and $B$ do not have opposite sign. Assuming that the problem has a solution in the first place, there is only one.

To prove that, it must be proved that any two solutions $u_1$ and $u_2$ of the same problem cannot be different. That they must be the same. In other words, it must be proved that the difference $v=u_1-u_2$ between any two solutions $u_1$ and $u_2$ is zero.

The proof starts with deriving the equations satisfied by the difference $v$. Since by assumption $u_1$ and $u_2$ are both solutions of the same problem:

$$\nabla^2 u_2 = f \quad\mbox{in}\quad \Omega \qquad A u... ...rtial u_2}{\partial n} = g \quad\mbox{on}\quad \delta\Omega$$

$$\nabla^2 u_1 = f \quad\mbox{in}\quad \Omega \qquad A u... ...rtial u_1}{\partial n} = g \quad\mbox{on}\quad \delta\Omega$$

If you subtract these two problems from each other, and replace $u_2-u_1$ by $v$, you get

$$\nabla^2 v = 0 \quad\mbox{in}\quad \Omega \qquad A v +... ...partial v}{\partial n} = 0 \quad\mbox{on}\quad \delta\Omega$$

Note that both the partial differential equation and the boundary condition are homogeneous. That illustrates an important point:

The difference between two solutions of a problem always satisfies the homogeneous problem.

Now we must prove that $v$ is zero. That will mean that the difference between $u_1$ and $u_2$ is zero. And that will in turn imply that $u_1$ and $u_2$ must be the same; different solutions are not possible.

To prove that $v$ is zero, the trick is to multiply the Laplace equation for $v$ by $-v$ and integrate over the entire domain $\Omega$:

$$- \int_{\Omega} v \nabla^2 v { \rm d}V = 0$$

Now note that, (assuming three dimensions, with $(x,y,z)=(x_1,x_2,x_3)$),

$$v \nabla^2 v = v \sum_{i=1}^3 \frac{\partial^2 v}{\partial... ...ight)^2 = \nabla\cdot (v\nabla v) - \left(\nabla v\right)^2$$

(If you do not believe the second equals sign, just differentiate out the product immediately to the right of it.) Plugging this into the equation above gives

$$\mbox{}- \int_{\Omega} \nabla\cdot(v \nabla v) { \rm d}V + \int_{\Omega}\left(\nabla v\right)^2 { \rm d}V = 0$$

And now apply the divergence (or Gauss or Ostrogradski) theorem on the first integral to get

$$\mbox{} - \int_{\delta\Omega} v \frac{\partial v}{\partial... ...}S + \int_{\Omega}\left(\nabla v\right)^2 { \rm d}V = 0 %$$ (1.19)

Note that the second integral is physically a potential energy in some important cases, like for a membrane under tension.

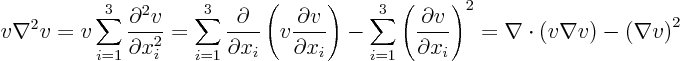
Now consider some special cases, starting with the simplest one:

• The Dirichlet problem: For the Dirichlet problem, $v$ is zero on the boundary. So the first integral is zero. What is left is
  
  $$\int_{\Omega}\left(\nabla v\right)^2 { \rm d}V = 0$$
  
  
  This can only be true if $\nabla{v}=0$ everywhere. For assume the opposite, that $\nabla{v}$ was nonzero in some vicinity. In that case $(\nabla{v})^2$ would be positive in that vicinity. So the vicinity would give a positive contribution to the integral. To get zero for the complete integral, that positive contribution would have to be cancelled by a negative contribution elsewhere. But $(\nabla{v})^2$ cannot be negative, so negative contributions to the integral are impossible.

  So $\nabla{v}$ must be zero everywhere, and that means that $v$ must equal some constant $C$ everywhere. That includes that $v$ must be $C$ on the boundary. But $v=0$ on the boundary, so $C$ must be zero. So $v$ is everywhere zero. So the difference between any two solutions $u_1$ and $u_2$ of the original problem must be everywhere zero. That means that the solutions must be equal, different solutions are not possible. So the solution is unique.

• The Neumann problem: For the Neumann problem, the first integral in (1.19) must again be zero, now because $\partial{v}/\partial{n}$ is zero on the boundary. So just like for the Dirichlet case above, $v$ must everywhere be equal to some constant $C$. However, this constant does not have to be zero in this case. The Neumann boundary condition is satisfied regardless of what $C$ is.

  So solutions of the Neumann problem are not unique. However, different solutions differ only by a constant, nothing more than that.

• The mixed problem with $A$ and $B$ of the same sign: For the mixed problem, you can use the boundary condition to write $\partial{v}/\partial{n}$ on the boundary in terms of $v$. That gives:
  

  $$\frac{A}{B} \int_{\delta\Omega} v^2 { \rm d}S + \int_{\Omega}\left(\nabla v\right)^2 { \rm d}V = 0$$ (1.20)

  
  
  If $A$ and $B$ are of the same sign, you can use this to show that the solution is unique.

  To do that, note that in that case the final integral must again be zero. The final integral cannot be negative because it is an integral of a square. And the final integral cannot be positive; otherwise the first term in the sum above would have to be negative to make their sum zero. And the first term cannot be negative because it too is an integral of a square.

  Since the second integral is zero, $v$ must again be some constant $C$. And since $A$ is nonzero at at least some point, (otherwise it would be the pure Neumann problem), it follows from the boundary condition that the constant is zero. So like the Dirichlet problem, the solution is unique.

• Varying boundary conditions: You could have a problem where, say, on parts of the boundary a Dirichlet condition is satisfied, on other parts a Neumann condition, and on still other parts a mixed condition.

  In that case, the first, surface, integral in (1.19) is a sum over all these parts. As long as you can show that the combined integral is zero or negative, $v$ must be zero and the solution is unique. (Except that in the pure Neumann case, the solution is indeterminate by a constant.)

• The eigenvalue problem: The eigenvalue problem for the Laplacian operator is
  
  $$\nabla^2 u = \lambda u \quad\mbox{in}\quad \Omega \qquad A u + B \frac{\partial u}{\partial n} = 0$$
  
  
  where the solution $u$ must be nonzero. Using the same steps as before for $v$, you get
  

  $$\mbox{} - \int_{\delta\Omega} u \frac{\partial u}{\partial... ...bla u\right)^2 { \rm d}V + \lambda \int_{\Omega} u^2 = 0$$ (1.21)

  
  
  From this it can be seen that for Dirichlet boundary conditions, or mixed boundary conditions with $A$ and $B$ of the same sign, the eigenvalues $\lambda$ can only be negative. For Neumann boundary conditions, the eigenvalues can only be negative or zero. The zero eigenvalue must correspond to constant $u$.

1.7.1 Review Questions

1

Show that the Poisson equation

$$\nabla^2 u = f$$

with boundary conditions

$$u_y(x,1)=g_1(x) \qquad u_y(x,0)=g_2(x)$$

$$u(0,y)=g_3(y) \qquad u(1,y)+u_x(1,y)=g_4(y)$$

has unique solutions.

Solution emp-a

2

Using the arguments given in the text, uniqueness can not be shown for the Poisson equation

$$\nabla^2 u = f$$

with boundary conditions

$$u_y(x,1)=g_1(x) \qquad u_y(x,0)=g_2(x)$$

$$u(0,y)=g_3(y) \qquad u(1,y)-u_x(1,y)=g_4(y)$$

Of course, just because you cannot prove uniqueness does not mean it is not true. But show that this problem never has unique solutions. If it has a solution at all, there are infinitely many different ones.

Solution emp-b

1.7.2 The heat equation

For the heat equation, similar arguments can be made as for the Laplace equation. This subsection briefly indicates the general lines.

Like for the Laplace equation in the previous subsection, the difference $v$ between any two solutions of a heat equation problem must satisfy the homogenous problem. That problem is here

$$v_t = \kappa \nabla^2 v \quad\mbox{in}\quad \Omega \qqua... ...n}\quad \delta\Omega \qquad v = 0 \quad\mbox{at}\quad t=0$$

Multiply the partial differential equation by $v$ and integrate like for the Laplace equation to get

$$\frac{{\rm d}}{{\rm d}t} \int_{\Omega} {\textstyle\frac{1}... ...+ \int_{\Omega} \kappa \left(\nabla v\right)^2 { \rm d}V = 0$$ (1.22)

Now consider conditions like those for the Laplace equation; Dirichlet or Neumann boundary conditions, or mixed boundary boundary conditions where $A$ and $B$ have the same sign. For those the final two terms cannot by negative. So the first term cannot be positive. So the “energy integral”

$$\int_{\Omega} {\textstyle\frac{1}{2}} v^2 { \rm d}V$$

cannot increase in time. Because of the initial condition, it starts at zero. If it cannot grow, it cannot become greater than zero. (And it cannot become less than zero because it is the integral of a positive quantity.) So the energy integral must stay zero for all time. And that is only possible if $v$ is everywhere zero for all time. If $v$ was somewhere nonzero, the energy integral would be positive.

If the difference between two solutions is always zero, different solutions are not possible. Solutions are unique.

Under the same conditions on the boundary conditions, you can see that one condition for properly posedness is satisfied: small changes in the initial conditions produce small changes in the solution. To see this, allow a nonzero initial condition for $v$ in the arguments above. The energy integral for $v$ at a later time is still never larger than the energy integral of the initial condition for $v$. And the energy integral is a measure for the magnitude of $v$: if you divide the energy integral by half the volume of the domain and take a square root, it gives the root mean square value of $v$.

1.7.3 The wave equation

For the wave equation, similar arguments can be made as for the Laplace and heat equations. This subsection briefly indicates the general lines.

Like in the previous two subsections, the difference $v$ between any two solutions of a wave equation problem must satisfy the homogenous problem. That problem is here

$$v_{tt} = a^2 \nabla^2 v \mbox{ in } \Omega \qquad A v ... ...box{ on } \delta\Omega \qquad v = v_t = 0 \mbox{ at } t=0$$

Multiply by $v_t$ and integrate over $\Omega$ as before using the divergence theorem to get

$$\frac{{\rm d}}{{\rm d}t} \int_{\Omega} {\textstyle\frac{1}... ...tyle\frac{1}{2}} a^2 \left(\nabla v\right)^2 { \rm d}V = 0$$ (1.23)

Now consider conditions like those for the Laplace equation; Dirichlet or Neumann boundary conditions, or mixed boundary boundary conditions where $A$ and $B$ have the same sign. Under such conditions the surface integral term cannot be negative. So the time derivative of the “energy integral”

$$\int_{\Omega} {\textstyle\frac{1}{2}} v_t^2 + {\textstyle\frac{1}{2}} a^2 \left(\nabla v\right)^2 { \rm d}V$$

is never positive; the energy integral cannot increase. So it must stay at its initial value of zero. So the spatial derivatives of $v$, as well as its time derivative, must be zero for all time. So $v$ must be a constant. And the initial condition says that that constant is zero. So $v$ is zero everywhere for all time.

If the difference between two solutions is always zero, different solutions are not possible. Solutions are unique.

It may be noted that physically, the first term in the energy equation is typically kinetic energy, and the second potential energy. If you generalize the problem for $v$ to still have homogeneous boundary conditions, but inhomogeneous initial conditions, you can derive energy conservation. In particular for homogeneous Dirichlet or Neumann boundary conditions, the total energy is preserved. For mixed boundary conditions where $A$ and $B$ have the same sign, the energy can only decrease. If $A$ and $B$ have opposite sign, the problem is unstable in the sense that the energy will increase. You can also use this to show that small changes in the initial conditions produce small changes in the solution for appropriate boundary conditions.