| Partial Differential Equations Solution Manual |
|
© Leon van Dommelen |
|
Question:
Using the arguments given in the text, uniqueness can not be shown for the Poisson equation
with boundary conditions
Of course, just because you cannot prove uniqueness does not mean it is not true. But show that this problem never has unique solutions. If it has a solution at all, there are infinitely many different ones.
Answer:
If you can show that the homogeneous problem has a nontrivial (nonzero) solution 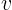 , you are done. Then if there is any solution
, you are done. Then if there is any solution  to the original problem, infinitely many more solutions can be obtained by adding arbitrary multiples of
to the original problem, infinitely many more solutions can be obtained by adding arbitrary multiples of 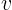 to
to  .
.
To find a nontrivial solution, guess it. In particular, based on the boundary conditions for 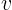 at
at 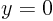 and
and 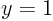 , guess that the nontrivial solution
, guess that the nontrivial solution 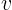 may be independent of
may be independent of 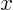 . If you plug that assumption into the partial differential equation and boundary conditions, you can indeed find a nonzero solution.
. If you plug that assumption into the partial differential equation and boundary conditions, you can indeed find a nonzero solution.
If you solve the problem for a general mixed boundary condition, using separation of variables, you find that for many values of the coefficients  and
and 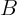 , but not all, there are nonunique solutions. However, there are none unless
, but not all, there are nonunique solutions. However, there are none unless  and
and 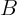 have opposite sign.
have opposite sign.
![]() , you are done. Then if there is any solution
, you are done. Then if there is any solution ![]() to the original problem, infinitely many more solutions can be obtained by adding arbitrary multiples of
to the original problem, infinitely many more solutions can be obtained by adding arbitrary multiples of ![]() to
to ![]() .
.
![]() at
at ![]() and
and ![]() , guess that the nontrivial solution
, guess that the nontrivial solution ![]() may be independent of
may be independent of ![]() . If you plug that assumption into the partial differential equation and boundary conditions, you can indeed find a nonzero solution.
. If you plug that assumption into the partial differential equation and boundary conditions, you can indeed find a nonzero solution.
![]() and
and ![]() , but not all, there are nonunique solutions. However, there are none unless
, but not all, there are nonunique solutions. However, there are none unless ![]() and
and ![]() have opposite sign.
have opposite sign.