| Partial Differential Equations Solution Manual |
|
© Leon van Dommelen |
|
Question:
Continuing the previous question, show analytically that for the supposed solution
the sum does not converge for any 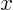 if
if  .
.
Also show analytically that at the halfway point 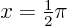 , the values that you get while summing increase monotonically to infinity.
, the values that you get while summing increase monotonically to infinity.
Answer:
Note that a requirement for a sum to converge is that the terms in the sum go to zero. Now apply good old l’Ho[s]pital, or equivalent, on 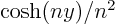 .
.
At the halfway point, you can show that the terms being summed are always positive, and that they grow bigger and bigger. So their sum grows bigger and bigger too. Therefore 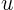 goes to infinity monotoneously.
goes to infinity monotoneously.
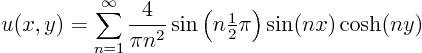
![]() , the values that you get while summing increase monotonically to infinity.
, the values that you get while summing increase monotonically to infinity.
![]() .
.
![]() goes to infinity monotoneously.
goes to infinity monotoneously.