| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
A.40 Deuteron wave function
This addendum examines the form of the wave function of the deuteron.
It assumes that the deuteron can be described as a two particle
system; a proton and a neutron. In reality, both the proton and the
neutron consist of three quarks. So the deuteron is really a six
particle system. That will be ignored here.
Then the deuteron wave function is a function of the positions and
spin angular momenta of the proton and neutron. That however can be
simplified considerably. First of all, it helps if the center of
gravity of the deuteron is taken as origin of the coordinate system.
In that coordinate system, the individual positions of proton and
neutron are no longer important. The only quantity that is important
is the position vector going from neutron to proton,
{A.5}:
That represents the relative position of the proton relative to the
neutron.
Consider now the spin angular momenta of proton and neutron. The two
have spin angular momenta of the same magnitude. The corresponding
quantum number, called the spin
for short, equals
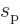

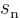

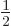 . However, the
proton and neutron can still have different spin angular momentum
along whatever is chosen to be the
. However, the
proton and neutron can still have different spin angular momentum
along whatever is chosen to be the  -axis. In particular, each can
have a spin
-axis. In particular, each can
have a spin 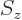 along the
along the  -axis that is either
-axis that is either 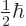 or
or
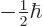 .
.
All together it means that the deuteron wave function depends
nontrivially on both the nucleon spacing and the spin components in
the  -direction:
-direction:
The square magnitude of this wave function gives the probability
density to find the nucleons at a given spacing  and with given
spin values along the
and with given
spin values along the  -axis.
-axis.
It is solidly established by experiments that the wave function of the
deuteron has net nuclear spin 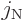
 1 and even parity. The
question to be examined now is what that means for the orbital angular
momentum and the spins of the proton and neutron. To answer that, the
wave function needs to be written in terms of states that have
definite combined orbital angular momentum and definite combined spin.
1 and even parity. The
question to be examined now is what that means for the orbital angular
momentum and the spins of the proton and neutron. To answer that, the
wave function needs to be written in terms of states that have
definite combined orbital angular momentum and definite combined spin.
The conditions for a state to have definite orbital angular momentum
were discussed in chapter 4.2. The angular dependence of
the state must be given by a spherical harmonic
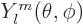 . Here
. Here  and
and  are the angles
that the vector
are the angles
that the vector  makes with the axes of the chosen spherical
coordinate system. The azimuthal quantum number
makes with the axes of the chosen spherical
coordinate system. The azimuthal quantum number  describes the
magnitude of the orbital angular momentum. In particular, the
magnitude of the orbital momentum is
describes the
magnitude of the orbital angular momentum. In particular, the
magnitude of the orbital momentum is 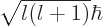 . The
magnetic quantum number
. The
magnetic quantum number  describes the component of the orbital
angular momentum along the chosen
describes the component of the orbital
angular momentum along the chosen  -axis. In particular, that
component equals
-axis. In particular, that
component equals 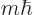 . Both
. Both 
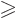 0 and
0 and 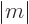
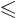
 must be integers.
must be integers.
As far as the combined spin angular momentum is concerned, the
possibilities were discussed in chapter 5.5.6 and in
more detail in chapter 12. First, the proton and
neutron spins can cancel each other perfectly, producing a state of
zero net spin. This state is called the singlet
state. Zero net spin has a corresponding quantum number 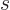
 0. And
since the component of the angular momentum along any chosen
0. And
since the component of the angular momentum along any chosen  -axis
can only be zero, so is the spin magnetic quantum number
-axis
can only be zero, so is the spin magnetic quantum number 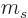
 0.
0.
The second possibility is that the proton and neutron align their
spins in parallel, crudely speaking. More precisely, the combined
spin has a magnitude given by quantum number 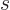

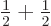
 1. The combined spin angular momentum along the chosen
1. The combined spin angular momentum along the chosen  direction is
direction is 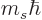 where
where 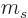 can be
can be  1, 0, or 1.
1, 0, or 1.
The wave function of the deuteron can be written as a combination of
the above states of orbital and spin angular momentum. It then takes
the generic form:
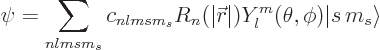 |
(A.257) |
Here the 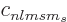 are constants. The functions
are constants. The functions 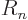 are not of
particular interest here; any complete set of orthonormal radial
functions will do. Note that the individual terms in the sum above
are not supposed to be energy eigenfunctions. They are merely chosen
states of definite orbital and spin angular momentum. The ket
are not of
particular interest here; any complete set of orthonormal radial
functions will do. Note that the individual terms in the sum above
are not supposed to be energy eigenfunctions. They are merely chosen
states of definite orbital and spin angular momentum. The ket
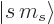 is a way of indicating the combined spin state of the
two nucleons. It is defined in terms of the separate spins of the
proton and neutron in chapter 5.5.6 (5.26).
is a way of indicating the combined spin state of the
two nucleons. It is defined in terms of the separate spins of the
proton and neutron in chapter 5.5.6 (5.26).
The above expression for the wave function is quite generally valid
for a system of two fermions. But it can be made much more specific
based on the mentioned known properties of the deuteron.
The simplest is the fact that the parity of the deuteron is even.
Spherical harmonics have odd parity if  is odd, and even if
is odd, and even if  is
even, {D.14}. So there cannot be any odd values of
is
even, {D.14}. So there cannot be any odd values of
 in the sum above. In other words, the constants
in the sum above. In other words, the constants 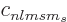 must be zero for odd
must be zero for odd  .
.
Physically, that means that the spatial wave function is symmetric
with respect to replacing  by
by 
 . It may be noted that
this spatial symmetry and the corresponding even parity are exactly
what is expected theoretically. The reasons were explored earlier in
{A.8} and {A.9}. The wave function
for any given spin state should not change sign, and odd parity cannot
meet that requirement. However, it should be noted that the arguments
in {A.8} and {A.9} are not valid if
the potential includes terms of second or higher order in the
momentum. Some more advanced potentials that have been written down
include such terms.
. It may be noted that
this spatial symmetry and the corresponding even parity are exactly
what is expected theoretically. The reasons were explored earlier in
{A.8} and {A.9}. The wave function
for any given spin state should not change sign, and odd parity cannot
meet that requirement. However, it should be noted that the arguments
in {A.8} and {A.9} are not valid if
the potential includes terms of second or higher order in the
momentum. Some more advanced potentials that have been written down
include such terms.
The spatial symmetry also means that the wave function is symmetric
with respect to swapping the two nucleons. That is because  is
the vector from neutron to proton, so swapping the two inverts the
sign of
is
the vector from neutron to proton, so swapping the two inverts the
sign of  . This does assume that the small difference in
mass between the neutron and proton is ignored. Otherwise the swap
would change the center of gravity. Recall that the (part of the)
wave function considered here is relative to the center of gravity.
In any case, the hypothetical wave functions for a bound state of two
protons or one of two neutrons would be exactly symmetric under
exchange of the positions of the two identical particles.
. This does assume that the small difference in
mass between the neutron and proton is ignored. Otherwise the swap
would change the center of gravity. Recall that the (part of the)
wave function considered here is relative to the center of gravity.
In any case, the hypothetical wave functions for a bound state of two
protons or one of two neutrons would be exactly symmetric under
exchange of the positions of the two identical particles.
The condition that the nuclear spin 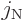
 1 is a bit more
complex. First a brief review is needed into how angular momenta
combine in quantum mechanics. (For a more complete description, see
chapter 12.) A state with definite quantum numbers
1 is a bit more
complex. First a brief review is needed into how angular momenta
combine in quantum mechanics. (For a more complete description, see
chapter 12.) A state with definite quantum numbers  and
and 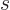 has in general quantum uncertainty in the net nuclear spin
has in general quantum uncertainty in the net nuclear spin
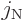 . But the values of
. But the values of 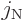 cannot be
completely arbitrary. The only values that can have nonzero
probability are in the range
cannot be
completely arbitrary. The only values that can have nonzero
probability are in the range
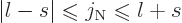
The key is now that unless a state 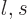 has a nonzero probability for
has a nonzero probability for
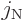
 1, it cannot appear in the deuteron wave function at all.
To verify that, take an inner product of the state with the
representation (A.257) of the deuteron wave function. In the
left hand side, you get zero because the deuteron wave function has
1, it cannot appear in the deuteron wave function at all.
To verify that, take an inner product of the state with the
representation (A.257) of the deuteron wave function. In the
left hand side, you get zero because the deuteron wave function has
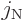
 1 and states of different
1 and states of different 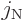 are orthogonal.
In the right hand side, all terms except one drop out because the
states in the sum are orthonormal. The one remaining term is the
coefficient of the considered state. Then this coefficient must be
zero since the left hand side is.
are orthogonal.
In the right hand side, all terms except one drop out because the
states in the sum are orthonormal. The one remaining term is the
coefficient of the considered state. Then this coefficient must be
zero since the left hand side is.
Using the above criterion, consider which states cannot appear in the
deuteron wave function. First of all, states with 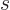
 0 are
according to the inequalities above states of nuclear spin
0 are
according to the inequalities above states of nuclear spin
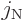

 . That cannot be 1, since
. That cannot be 1, since  had to be
even because of parity. So states with
had to be
even because of parity. So states with 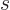
 0 cannot appear in
the deuteron wave function. It follows that the deuteron wave
function has a combined nucleon spin
0 cannot appear in
the deuteron wave function. It follows that the deuteron wave
function has a combined nucleon spin 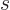
 1 without quantum
uncertainty.
1 without quantum
uncertainty.
Secondly, states with 
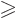 4 have
4 have 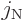 at least equal to 3
according to the above inequalities. So these states cannot appear.
That leaves only states with
at least equal to 3
according to the above inequalities. So these states cannot appear.
That leaves only states with 
 0 or 2 and
0 or 2 and 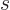
 1 as
possibilities.
1 as
possibilities.
Now states with 
 0 and
0 and 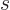
 1 are states with
1 are states with 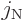
 1. Any such state can appear in the deuteron wave function. To
what amount remains unknown. That would only be answerable if an
exact solution to the proton-neutron deuteron would be available. But
surely, based on arguments like those in {A.8} and
{A.9}, it is to be expected that there is a
significant
1. Any such state can appear in the deuteron wave function. To
what amount remains unknown. That would only be answerable if an
exact solution to the proton-neutron deuteron would be available. But
surely, based on arguments like those in {A.8} and
{A.9}, it is to be expected that there is a
significant 
 0 component.
0 component.
States with 
 2 and
2 and 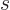
 1 are also a possibility. But
they cannot appear in arbitrary combinations. Any such state has
multiple possible values for
1 are also a possibility. But
they cannot appear in arbitrary combinations. Any such state has
multiple possible values for 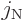 in the range from 1 to 3.
That uncertainty must be eliminated before the states are acceptable
for the deuteron wave function. It turns out that pure
in the range from 1 to 3.
That uncertainty must be eliminated before the states are acceptable
for the deuteron wave function. It turns out that pure 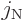
 1 states can be obtained by taking specific combinations of
states. In particular, groups of states that vary only in the quantum
numbers
1 states can be obtained by taking specific combinations of
states. In particular, groups of states that vary only in the quantum
numbers  and
and 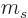 can be combined into states with
can be combined into states with 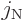
 1. (For the curious, the specific combinations needed can be
read off in figure 12.6).
1. (For the curious, the specific combinations needed can be
read off in figure 12.6).
The bottom line is that the deuteron wave function can have
uncertainty in the orbital angular momentum. In particular, both
orbital angular momentum numbers 
 0 and
0 and 
 2 can and do have a
nonzero probability.
2 can and do have a
nonzero probability.
![]()
![]()
![]()
![]()
![]() .
.![]() -
-![]()
![]() -
-![]()
![]() .
.![]() -
-![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() .
.![]()
![]() -
-![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() -
-![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 1
1![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]() .
.![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()