| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
A.9 Wave function symmetries
Symmetries are very important in physics. For example, symmetries in
wave functions are often quite helpful to understand the physics
qualitatively.
As an example, the hydrogen molecular ion is mirror symmetric around
its midplane. This midplane is the plane halfway in between the two
nuclei, orthogonal to the line connecting them. To roughly understand
what the mirror symmetry around this plane means, think of the
midplane as an infinitely thin mirror. Take this mirror to be
two-sided, so that you can look in it from either side. That allows
you to see the mirror image of each side of the molecule. Simply put,
the mirror symmetry of the ion means that the mirror image looks
exactly the same as the original ion.
(If you would place the entire molecule at one side of the mirror, its
entire mirror image would be at the other side of it. But except for
this additional shift in location, everything would remain the same as
in the case assumed here.)
Under the same terms, human beings are roughly mirror symmetric around
the plane separating their left and right halves. But that symmetry
is far from perfect. For example, if you part your hair at one side,
your mirror image parts it at the other side. And your heart changes
sides too.
To describe mirror symmetry more precisely, take the line through the
nuclei to be the  -axis. And take
-axis. And take  to be zero at the
mirror. Then all that the mirror does mathematically is replace
to be zero at the
mirror. Then all that the mirror does mathematically is replace  by
by 
 . For example, the mirror image of the nucleus at
positive
. For example, the mirror image of the nucleus at
positive  is located at the corresponding negative
is located at the corresponding negative  value.
And vice-versa.
value.
And vice-versa.
The effect of mirroring on any molecular wave function 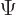 can be
represented by a “mirror operator”
can be
represented by a “mirror operator” 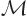 . According to the above, all
this operator does is replace
. According to the above, all
this operator does is replace  by
by 
 :
:
By definition a wave function is mirror symmetric if the mirror
operator has no effect on it. Mathematically, if the mirror
operator does not do anything, then 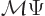 must be the same as
must be the same as
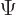 . So mirror symmetry requires
. So mirror symmetry requires
The final equality above shows that a mirror-symmetric wave function
is the same at positive values of  as at the corresponding negative
values. Mathematicians might simply say that the wave function is
symmetric around the
as at the corresponding negative
values. Mathematicians might simply say that the wave function is
symmetric around the 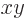 -plane, (i.e. the mirror). The ground
state
-plane, (i.e. the mirror). The ground
state  of the molecular ion is mirror symmetric in this
sense. The big question to be addressed in this addendum is, why?
of the molecular ion is mirror symmetric in this
sense. The big question to be addressed in this addendum is, why?
The fundamental reason why the ion is mirror symmetric is a
mathematical one. The mirror operator 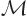 commutes with the
Hamiltonian
commutes with the
Hamiltonian 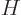 . Recall from chapter 4.5.1 what
this means:
. Recall from chapter 4.5.1 what
this means:
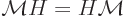
In words, it does not make a difference in which order you apply the
two operators.
That can be seen from the physics. The Hamiltonian consists of
potential energy  and kinetic energy
and kinetic energy  . Now it does not
make a difference whether you multiply a wave function value by the
potential before or after you flip the value over to the opposite
. Now it does not
make a difference whether you multiply a wave function value by the
potential before or after you flip the value over to the opposite
 -position. The potential is the same at opposite
-position. The potential is the same at opposite  values,
because the nuclei at the two sides of the mirror are the same. As
far as the kinetic energy is concerned, if it involved a first-order
values,
because the nuclei at the two sides of the mirror are the same. As
far as the kinetic energy is concerned, if it involved a first-order
 -derivative, there would be a change of sign when you flip
over the sign of
-derivative, there would be a change of sign when you flip
over the sign of  . But the kinetic energy has only a second
order
. But the kinetic energy has only a second
order  -derivative. A second order derivative does not
change. So all together it makes no difference whether you first
mirror and then apply the Hamiltonian or vice-versa. The two
operators commute.
-derivative. A second order derivative does not
change. So all together it makes no difference whether you first
mirror and then apply the Hamiltonian or vice-versa. The two
operators commute.
Also according to chapter 4.5.1, that has a consequence.
It implies that you can take energy eigenfunctions to be mirror
eigenfunctions too. And the ground state is an energy eigenfunction.
So it can be taken to be an eigenfunction of 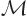 too:
too:
Here 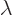 is a constant called the eigenvalue. But what would
this eigenvalue be?
is a constant called the eigenvalue. But what would
this eigenvalue be?
To answer that, apply 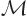 twice. That multiplies the wave
function by the square eigenvalue. But if you apply
twice. That multiplies the wave
function by the square eigenvalue. But if you apply 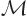 twice, you
always get the original wave function back, because
twice, you
always get the original wave function back, because 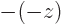

 . So the square eigenvalue
. So the square eigenvalue 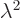 must be 1, in order
that the wave function does not change when multiplied by it. That
means that the eigenvalue
must be 1, in order
that the wave function does not change when multiplied by it. That
means that the eigenvalue 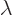 itself can be either 1 or
itself can be either 1 or  1. So
for the ground state wave function
1. So
for the ground state wave function  , either
, either
or
If the first possibility applies, the wave function does not change
under the mirroring. So by definition it is mirror symmetric. If the
second possibility applies, the wave function changes sign under the
mirroring. Such a wave function is called “mirror
antisymmetric.” But the second possibility has wave
function values of opposite sign at opposite values of  .
That is not possible, because the previous addendum showed that the
ground state wave function is everywhere positive. So it must be
possibility one. That means that the ground state must indeed be
mirror symmetric as claimed.
.
That is not possible, because the previous addendum showed that the
ground state wave function is everywhere positive. So it must be
possibility one. That means that the ground state must indeed be
mirror symmetric as claimed.
It may be noted that the state of second lowest energy will be
antisymmetric. You can see the same thing happening for the
eigenfunctions of the particle in a pipe. The ground state figure
3.8, (or 3.11 in three dimensions), is
symmetric around the center cross-section of the pipe. The first
excited state, at the top of figures 3.9, (or
3.12), is antisymmetric. (Note that the grey tones show
the square wave function. If the wave function is antisymmetric, the
square wave function is symmetric. But it will be zero at the
symmetry plane.)
Next consider the rotational symmetry of the hydrogen molecular ion
around the axis through the nuclei. The ground state of the molecular
ion does not change if you rotate the ion around the  -axis through
the nuclei. That makes it rotationally symmetric. The big question
is again, why?
-axis through
the nuclei. That makes it rotationally symmetric. The big question
is again, why?
In this case, let 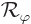 be the operator that rotates a wave
function
be the operator that rotates a wave
function 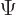 over an angle
over an angle 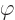 around the
around the  -axis. This
operator too commutes with the Hamiltonian. After all, the only
physically meaningful direction is the
-axis. This
operator too commutes with the Hamiltonian. After all, the only
physically meaningful direction is the  -axis through the nuclei.
The angular orientation of the
-axis through the nuclei.
The angular orientation of the 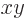 axes system normal to it is a
completely arbitrary choice. So it should not make a difference at
what angle around the
axes system normal to it is a
completely arbitrary choice. So it should not make a difference at
what angle around the  axis you apply the Hamiltonian.
axis you apply the Hamiltonian.
Therefore the ground state must be an eigenfunction of the rotation
operator just like it is one of the mirror operator:
But now what is that eigenvalue 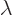 ? First note that the
magnitude of all eigenvalues of
? First note that the
magnitude of all eigenvalues of 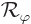 must be 1. Otherwise
the magnitude of the wave function would change correspondingly
during the rotation. However, the magnitude of a wave function does
not change if you simply rotate it. And if the eigenvalue is a
complex number of magnitude 1, then it can always be written as
must be 1. Otherwise
the magnitude of the wave function would change correspondingly
during the rotation. However, the magnitude of a wave function does
not change if you simply rotate it. And if the eigenvalue is a
complex number of magnitude 1, then it can always be written as
 where
where 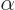 is some real number. So the rotated
ground state is some multiple
is some real number. So the rotated
ground state is some multiple  of the original ground
state. But the values of the rotated ground state are real and
positive just like that of the original ground state. That can only
be true if the multiplying factor
of the original ground
state. But the values of the rotated ground state are real and
positive just like that of the original ground state. That can only
be true if the multiplying factor  is real and positive
too. And if you check the Euler formula (2.5), you see
that
is real and positive
too. And if you check the Euler formula (2.5), you see
that  is only real and positive if it is 1. Since
multiplying by 1 does not change the wave function, the ground state
does not change when rotated. That then makes it rotationally
symmetric around the
is only real and positive if it is 1. Since
multiplying by 1 does not change the wave function, the ground state
does not change when rotated. That then makes it rotationally
symmetric around the  -axis through the nuclei as claimed.
-axis through the nuclei as claimed.
You might of course wonder about the rotational changes of excited
energy states. For those a couple of additional observations apply.
First, the number 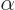 must be proportional to the rotation
angle
must be proportional to the rotation
angle 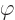 , since rotating
, since rotating 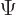 twice is equivalent to
rotating it once over twice the angle. That means that, more
precisely, the eigenvalues are of the form
twice is equivalent to
rotating it once over twice the angle. That means that, more
precisely, the eigenvalues are of the form
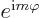 , where
, where  is a real constant independent of
is a real constant independent of
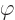 . Second, rotating the ion over a
. Second, rotating the ion over a 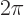 full turn
puts each point back to where it came from. That should reproduce
the original wave function. So an eigenvalue
full turn
puts each point back to where it came from. That should reproduce
the original wave function. So an eigenvalue 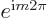 for a
full turn must be 1. According to the Euler formula, that requires
for a
full turn must be 1. According to the Euler formula, that requires
 to be an integer, one of ...,
to be an integer, one of ...,  2,
2,  1, 0, 1, 2, .... For
the ground state,
1, 0, 1, 2, .... For
the ground state,  will have to be zero; that is the only way to
get
will have to be zero; that is the only way to
get 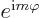 equal to 1 for all angles
equal to 1 for all angles 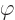 .
But for excited states,
.
But for excited states,  can be a nonzero integer. In that case,
these states do not have rotational symmetry.
can be a nonzero integer. In that case,
these states do not have rotational symmetry.
Recalling the discussion of angular momentum in chapter
4.2.2, you can see that  is really the magnetic quantum
number of the state. Apparently, there is a connection between
rotations around the
is really the magnetic quantum
number of the state. Apparently, there is a connection between
rotations around the  -axis and the angular momentum in the
-axis and the angular momentum in the
 -direction. That will be explored in more detail in chapter
7.3.
-direction. That will be explored in more detail in chapter
7.3.
For the neutral hydrogen molecule discussed in chapter 5.2,
there is still another symmetry of relevance. The neutral molecule
has two electrons, instead of just one. This allows another
operation: you can swap the two electrons. That is called “particle exchange.” Mathematically, what the particle
exchange operator 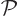 does with the wave function is swap the
position coordinates of electron 1 with those of electron 2.
Obviously, physically this does not do anything at all; the two
electrons are exactly the same. It does not make a difference which
of the two is where. So particle exchange commutes again with the
Hamiltonian.
does with the wave function is swap the
position coordinates of electron 1 with those of electron 2.
Obviously, physically this does not do anything at all; the two
electrons are exactly the same. It does not make a difference which
of the two is where. So particle exchange commutes again with the
Hamiltonian.
The mathematics of the particle exchange is similar to that of the
mirroring discussed above. In particular, if you exchange the
particles twice, they are back to where they were originally. From
that, just like for the mirroring, it can be seen that swapping the
particle positions does nothing to the ground state. So the ground
state is symmetric under particle exchange.
It should be noted that the ground state of systems involving three or
more electrons is not symmetric under exchanging the positions
of the electrons. Wave functions for multiple electrons must satisfy
special particle-exchange requirements, chapter 5.6. In
fact they must be antisymmetric under an expanded
definition of the exchange operator. This is also true for systems
involving three or more protons or neutrons. However, for some
particle types, like three or more helium atoms, the symmetry under
particle exchange continues to apply. This is very helpful for
understanding the properties of superfluid helium,
[18, p. 321].
![]() -
-![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]() .
.![]()
![]()
![]() :
:![]()
![]() .
.![]()
![]() .
.![]()
![]() .
.![]() -
-![]()
![]() -
-![]() .
.![]() -
-![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]() 1
1![]() ,
,![]() -
-![]()
![]()
![]()
![]() -
-![]() -
-![]()
![]()
![]()
![]() ,
,![]()
![]() ,
,![]()
![]() .
.![]()
![]()
![]()
![]() 2
2![]() 1
1![]()
![]()
![]() .
.![]()
![]()
![]() -
-![]() -
-![]()