| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.81 Dirac fine structure Hamiltonian
This note derives the fine structure Hamiltonian of the hydrogen atom.
This Hamiltonian fixes up the main relativistic errors in the
classical solution of chapter 4.3. The derivation is based
on the relativistic Dirac equation from chapter 12.12 and
uses nontrivial linear algebra.
According to the Dirac equation, the relativistic Hamiltonian and wave
function take the form
where 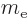 is the mass of the electron when at rest,
is the mass of the electron when at rest, 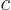 the speed of
light, and the
the speed of
light, and the 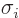 are the 2
are the 2  2 Pauli spin matrices of
chapter 12.10. Similarly the ones and zeros in the shown
matrices are 2
2 Pauli spin matrices of
chapter 12.10. Similarly the ones and zeros in the shown
matrices are 2  2 unit and zero matrices. The wave function
is a four-dimensional vector whose components depend on spatial position.
It can be subdivided into the two-dimensional vectors
2 unit and zero matrices. The wave function
is a four-dimensional vector whose components depend on spatial position.
It can be subdivided into the two-dimensional vectors 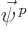 and
and
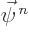 . The two components of
. The two components of 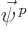 correspond to the spin up and spin down components of the normal
classical electron wave function; as noted in chapter
5.5.1, this can be thought of as a vector if you want.
The two components of the other vector
correspond to the spin up and spin down components of the normal
classical electron wave function; as noted in chapter
5.5.1, this can be thought of as a vector if you want.
The two components of the other vector 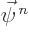 are very small
for the solutions of interest. These components would be dominant for
states that would have negative rest mass. They are associated with
the anti-particle of the electron, the positron.
are very small
for the solutions of interest. These components would be dominant for
states that would have negative rest mass. They are associated with
the anti-particle of the electron, the positron.
The Dirac equation is solvable in closed form, but that solution is
not something you want to contemplate if you can avoid it. And there
is really no need for it, since the Dirac equation is not exact
anyway. To the accuracy it has, it can easily be solved using
perturbation theory in essentially the same way as in derivation
{D.79}. In this case, the small parameter is
1/ : if the speed of light is infinite, the nonrelativistic
solution is exact. And if you ballpark a typical velocity for the
electron in a hydrogen atom, it is only about one percent or so of the
speed of light.
: if the speed of light is infinite, the nonrelativistic
solution is exact. And if you ballpark a typical velocity for the
electron in a hydrogen atom, it is only about one percent or so of the
speed of light.
So, following derivation {D.79}, take the Hamiltonian apart into
successive powers of 1
 as
as 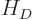

 with
with
and similarly for the wave function vector:
and the energy:
Substitution into the Hamiltonian eigenvalue problem
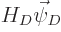

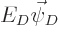 and then collecting equal powers of 1
and then collecting equal powers of 1
 together produces again a system of successive equations, just like
in derivation {D.79}:
together produces again a system of successive equations, just like
in derivation {D.79}:
The first, order 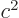 , eigenvalue problem has energy
eigenvalues
, eigenvalue problem has energy
eigenvalues 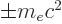 , in other words, plus or minus the
rest mass energy of the electron. The solution of interest is the
physical one with a positive rest mass, so the desired solution is
, in other words, plus or minus the
rest mass energy of the electron. The solution of interest is the
physical one with a positive rest mass, so the desired solution is
Plug that into the order 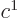 equation to give, for top and
bottom subvectors
equation to give, for top and
bottom subvectors
It follows from the first of those that the first order energy change
must be zero because 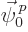 cannot be zero; otherwise there
would be nothing left. The second equation gives the leading order
values of the secondary components, so in total
cannot be zero; otherwise there
would be nothing left. The second equation gives the leading order
values of the secondary components, so in total
where the summation index  was renamed to
was renamed to  to avoid ambiguity
later.
to avoid ambiguity
later.
Plug all that in the order  equation to give
equation to give
The first of these two equations is the nonrelativistic Hamiltonian
eigenvalue problem of chapter 4.3. To see that, note that
in the double sum the terms with 
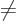
 pairwise cancel since
for the Pauli matrices,
pairwise cancel since
for the Pauli matrices, 
 0
when
0
when 
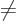
 . For the remaining terms in which
. For the remaining terms in which 

 , the relevant property of the Pauli matrices is that
, the relevant property of the Pauli matrices is that
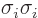 is one (or the 2
is one (or the 2 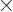 2 unit matrix, really,)
giving
2 unit matrix, really,)
giving
where 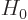 is the nonrelativistic hydrogen Hamiltonian of chapter
4.3.
is the nonrelativistic hydrogen Hamiltonian of chapter
4.3.
So the first part of the order  equation takes the form
equation takes the form
The energy 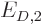 will therefore have to be a Bohr energy level
will therefore have to be a Bohr energy level
 and each component of
and each component of 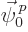 will have to be a
nonrelativistic energy eigenfunction with that energy:
will have to be a
nonrelativistic energy eigenfunction with that energy:
The sum multiplying 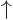 is the first component of vector
is the first component of vector
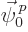 and the sum multiplying
and the sum multiplying 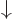 the second. The
nonrelativistic analysis in chapter 4.3 was indeed correct
as long as the speed of light is so large compared to the relevant
velocities that 1
the second. The
nonrelativistic analysis in chapter 4.3 was indeed correct
as long as the speed of light is so large compared to the relevant
velocities that 1
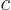 can be ignored.
can be ignored.
To find out the error in it, the relativistic expansion must be taken
to higher order. To order 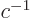 , you get for the top vector
, you get for the top vector
Now if 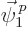 is written as a sum of the eigenfunctions of
is written as a sum of the eigenfunctions of
 , including
, including 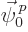 , the first term will
produce zero times
, the first term will
produce zero times 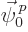 since
since
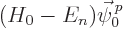
 0. That means that
0. That means that 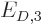 must
be zero. The expansion must be taken one step further to identify the
relativistic energy change. The bottom vector gives
must
be zero. The expansion must be taken one step further to identify the
relativistic energy change. The bottom vector gives
To order  , you get for the top vector
, you get for the top vector
and that determines the approximate relativistic energy correction.
Now recall from derivation {D.79} that if you do a
nonrelativistic expansion of an eigenvalue problem 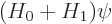

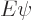 , the equations to solve are (D.55) and
(D.56);
, the equations to solve are (D.55) and
(D.56);
The first equation was satisfied by the solution for
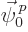 obtained above. However, the second equation
presents a problem. Comparison with the final Dirac result suggests
that the fine structure Hamiltonian correction
obtained above. However, the second equation
presents a problem. Comparison with the final Dirac result suggests
that the fine structure Hamiltonian correction 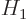 should be
identified as
should be
identified as
but that is not right, since  is not a physical operator, but an
energy eigenvalue for the selected eigenfunction. So mapping the
Dirac expansion straightforwardly onto a classical one has run into a
snag.
is not a physical operator, but an
energy eigenvalue for the selected eigenfunction. So mapping the
Dirac expansion straightforwardly onto a classical one has run into a
snag.
It is maybe not that surprising that a two-dimensional wave function cannot
correctly represent a truly four-dimensional one. But clearly,
whatever is selected for the fine structure Hamiltonian 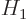 must at
least get the energy eigenvalues right. To see how this can be done,
the operator obtained from the Dirac equation will have to be
simplified. Now for any given
must at
least get the energy eigenvalues right. To see how this can be done,
the operator obtained from the Dirac equation will have to be
simplified. Now for any given  , the sum over
, the sum over  includes a
term
includes a
term 

 , a term
, a term 

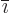 , where
, where 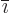 is
the number following
is
the number following  in the cyclic sequence
in the cyclic sequence
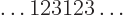 , and it involves a term
, and it involves a term 

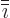 where
where 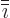 precedes
precedes  in the sequence. So the Dirac operator
falls apart into three pieces:
in the sequence. So the Dirac operator
falls apart into three pieces:
or using the properties of the Pauli matrices that 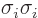
 1,
1, 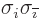

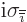 , and
, and
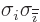

 for any
for any  ,
,
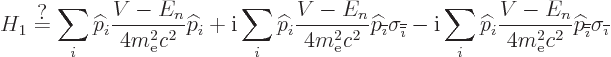 |
(D.59) |
The approach will now be to show first that the final two terms are
the spin-orbit interaction in the fine structure Hamiltonian. After
that, the much more tricky first term will be discussed. Renotate
the indices in the last two terms as follows:
Since the relative order of the subscripts in the cycle was maintained
in the renotation, the sums still contain the exact same three terms,
just in a different order. Take out the common factors;
Now according to the generalized canonical commutator of chapter
4.5.4:
where  is a constant that produces a zero derivative. So
is a constant that produces a zero derivative. So
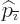 , respectively
, respectively 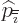 can be taken to the other
side of
can be taken to the other
side of  as long as the appropriate derivatives of
as long as the appropriate derivatives of  are
added. If that is done,
are
added. If that is done, 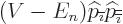 and
and
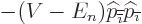 cancel since linear momentum operators
commute. What is left are just the added derivative terms:
cancel since linear momentum operators
commute. What is left are just the added derivative terms:
Note that the errant eigenvalue  mercifully dropped out. Now the
hydrogen potential
mercifully dropped out. Now the
hydrogen potential  only depends on the distance
only depends on the distance  from the
origin, as 1/
from the
origin, as 1/ , so
, so
and plugging that into the operator, you get
The term between the square brackets can be recognized as the  th
component of the angular momentum operator; also the Pauli spin matrix
th
component of the angular momentum operator; also the Pauli spin matrix
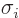 is defined as
is defined as 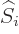

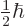 , so
, so
Get rid of 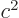 using
using 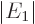

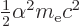 ,
of
,
of  using
using 

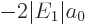

 , and
, and 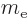 using
using 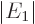

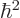

 to get the spin-orbit interaction as
claimed in the section on fine structure.
to get the spin-orbit interaction as
claimed in the section on fine structure.
That leaves the term
in (D.59). Since 

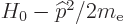 , it can be
written as
, it can be
written as
The final term is the claimed Einstein correction in the fine
structure Hamiltonian, using 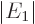

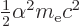 to get rid of
to get rid of 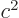 .
.
The first term,
is the sole remaining problem. It cannot be transformed into a decent
physical operator. The objective is just to get the energy correction
right. And to achieve that requires only that the Hamiltonian
perturbation coefficients are evaluated correctly at the  energy
level. Specifically, what is needed is that
energy
level. Specifically, what is needed is that
for any arbitrary pair of unperturbed hydrogen energy eigenfunctions
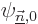 and
and 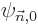 with energy
with energy  . To see
what that means, the leading Hermitian operator
. To see
what that means, the leading Hermitian operator 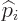 can be taken to
the other side of the inner product, and in half of that result,
can be taken to
the other side of the inner product, and in half of that result,
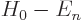 will also be taken to the other side:
will also be taken to the other side:
Now if you simply swap the order of the factors in 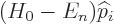 in
this expression, you get zero, because both eigenfunctions have energy
in
this expression, you get zero, because both eigenfunctions have energy
 . However, swapping the order of
. However, swapping the order of 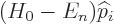 brings in
the generalized canonical commutator
brings in
the generalized canonical commutator ![$[V,{\widehat p}_i]$](img7669.gif) that equals
that equals


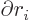 . Therefore, writing out
the remaining inner product you get
. Therefore, writing out
the remaining inner product you get
Now, the potential  becomes infinite at
becomes infinite at 
 0, and that makes
mathematical manipulation difficult. Therefore, assume for now that
the nuclear charge
0, and that makes
mathematical manipulation difficult. Therefore, assume for now that
the nuclear charge 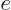 is not a point charge, but spread out over a
very small region around the origin. In that case, the inner product
can be rewritten as
is not a point charge, but spread out over a
very small region around the origin. In that case, the inner product
can be rewritten as
and the first term integrates away since 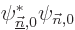 vanishes at infinity. In the final term, use the fact that the
derivatives of the potential energy
vanishes at infinity. In the final term, use the fact that the
derivatives of the potential energy  give
give 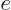 times the electric
field of the nucleus, and therefore the second order derivatives give
times the electric
field of the nucleus, and therefore the second order derivatives give
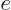 times the divergence of the electric field. Maxwell’s first
equation (13.5) says that that is
times the divergence of the electric field. Maxwell’s first
equation (13.5) says that that is 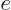

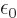 times
the nuclear charge density. Now if the region of nuclear charge is
allowed to contract back to a point, the charge density must still
integrate to the net proton charge
times
the nuclear charge density. Now if the region of nuclear charge is
allowed to contract back to a point, the charge density must still
integrate to the net proton charge 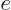 , so the charge density
becomes
, so the charge density
becomes 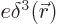 where
where 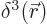 is the three-dimensional
delta function. Therefore the Darwin term produces Hamiltonian
perturbation coefficients as if its Hamiltonian is
is the three-dimensional
delta function. Therefore the Darwin term produces Hamiltonian
perturbation coefficients as if its Hamiltonian is
Get rid of  using
using 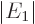

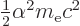 ,
of
,
of 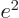

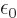 using
using 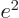

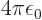

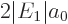 , and
, and 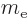 using
using 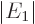

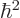

 to get the Darwin term as claimed in the
section on fine structure. It will give the right energy correction
for the nonrelativistic solution. But you may rightly wonder what to
make of the implied wave function.
to get the Darwin term as claimed in the
section on fine structure. It will give the right energy correction
for the nonrelativistic solution. But you may rightly wonder what to
make of the implied wave function.
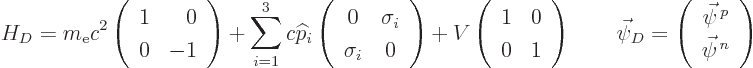
![]() :
:![]()
![]()
![]()
![]()
![]()
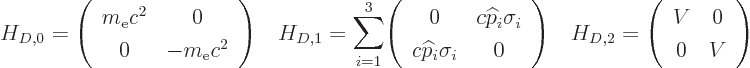
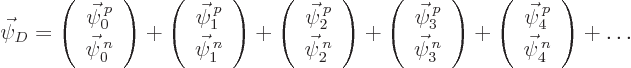
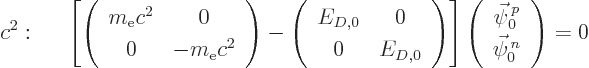
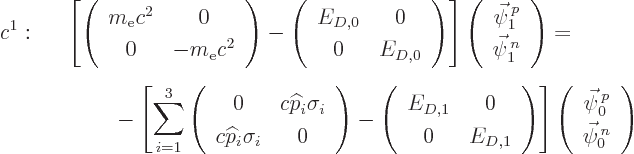

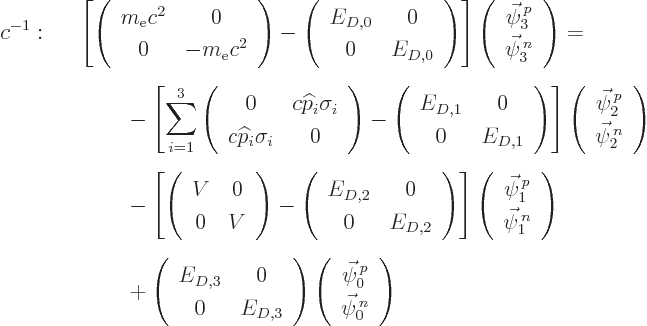
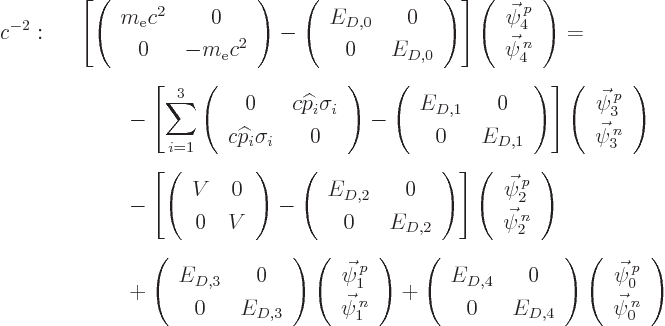
![]() ,
,![]() ,
,
![]()
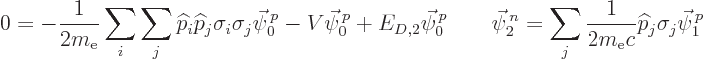
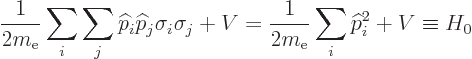
![]()
![]() ,
,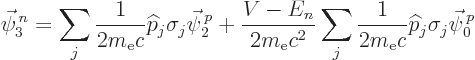
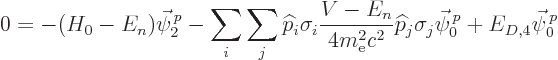
![]()
![]()
![]() ,
,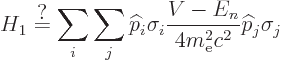
![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
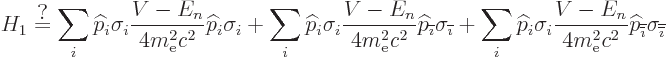
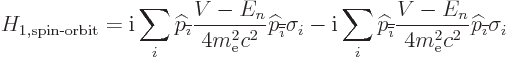
![\begin{displaymath}
H_{1,\mbox{\scriptsize spin-orbit}} =
\frac{{\rm i}}{4m_{\...
...}}}}(V-E_n){\widehat p}_{{\overline{\imath}}}\right]\sigma_{i}
\end{displaymath}](img7647.gif)
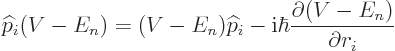
![\begin{displaymath}
H_{1,\mbox{\scriptsize spin-orbit}} =
\frac{\hbar}{4m_{\rm...
...math}}}}}{\widehat p}_{{\overline{\imath}}}
\right]\sigma_{i}
\end{displaymath}](img7654.gif)
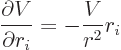
![\begin{displaymath}
H_{1,\mbox{\scriptsize spin-orbit}} =
- \frac{\hbar V}{4m_...
...{\imath}}}}{\widehat p}_{{\overline{\imath}}}\right]\sigma_{i}
\end{displaymath}](img7656.gif)
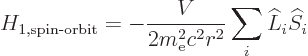


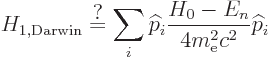


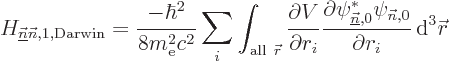
![\begin{displaymath}
H_{\underline{\vec n}{\vec n},1,{\rm Darwin}} = \frac{-\hba...
...ec n},0}^*\psi_{{\vec n},0}
\right] { \rm d}^3{\skew0\vec r}
\end{displaymath}](img7672.gif)