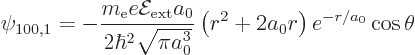| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.80 Hydrogen ground state Stark effect
This note derives the Stark effect on the hydrogen ground state.
Since spin is irrelevant for the Stark effect, it will be ignored.
The unperturbed ground state of hydrogen was derived in chapter
4.3. Following the convention in perturbation theory to
append a subscript zero to the unperturbed state, it can be summarized
as:
where 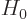 is the unperturbed hydrogen atom Hamiltonian,
is the unperturbed hydrogen atom Hamiltonian,
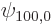 the unperturbed ground state wave function,
the unperturbed ground state wave function, 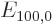 the unperturbed ground state energy, 13.6 eV, and
the unperturbed ground state energy, 13.6 eV, and 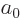 is the Bohr
radius, 0.53 Å.
is the Bohr
radius, 0.53 Å.
The Stark perturbation produces a change 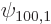 in this wave
function that satisfies, from (A.243),
in this wave
function that satisfies, from (A.243),
The first order energy change 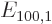 is zero and can be dropped.
The solution for
is zero and can be dropped.
The solution for 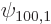 will now simply be guessed to be
will now simply be guessed to be
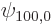 times some spatial function
times some spatial function  still to be found:
still to be found:
Differentiating out the Laplacian  of the product
of the product
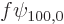 into individual terms using Cartesian coordinates, the
equation becomes
into individual terms using Cartesian coordinates, the
equation becomes
The first term in this equation is zero since 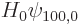

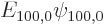 . Also, now using spherical coordinates,
the gradients are, e.g. [41, 20.74, 20.82],
. Also, now using spherical coordinates,
the gradients are, e.g. [41, 20.74, 20.82],
Substituting that into the equation, it reduces to
Now 

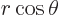 in polar coordinates, and for the
in polar coordinates, and for the
 -derivative of
-derivative of  to produce something that is proportional
to
to produce something that is proportional
to  ,
,  must be proportional to
must be proportional to 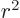 . (The Laplacian
in the second term always produces lower powers of
. (The Laplacian
in the second term always produces lower powers of  than the
than the
 -derivative and can for now be ignored.) So, to balance the
right hand side,
-derivative and can for now be ignored.) So, to balance the
right hand side,  should contain a highest power of
should contain a highest power of  equal to:
equal to:
but then, using [41, 20.83], the 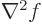 term in the
left hand side produces an
term in the
left hand side produces an 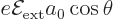 term. So
add another term to
term. So
add another term to  for its
for its  -derivative to eliminate it:
-derivative to eliminate it:
The Laplacian of 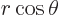

 is zero so no further terms
need to be added. The change
is zero so no further terms
need to be added. The change 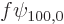 in wave function is
therefore
in wave function is
therefore
(This small perturbation
becomes larger than the
unperturbed wave function far from the atom because of the growing
value of 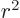 . It is implicitly assumed that the electric
field terminates before a real problem arises. This is related to the
possibility of the electron tunneling out of the atom if the potential
far from the atom is less than its energy in the atom: if the electron
can tunnel out, there is strictly speaking no bound state.)
. It is implicitly assumed that the electric
field terminates before a real problem arises. This is related to the
possibility of the electron tunneling out of the atom if the potential
far from the atom is less than its energy in the atom: if the electron
can tunnel out, there is strictly speaking no bound state.)
Now according to (A.243), the second order energy change
can be found as
Doing the inner product integration in spherical coordinates produces
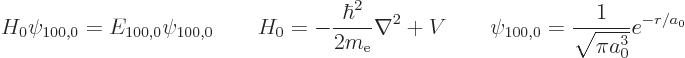
![]()
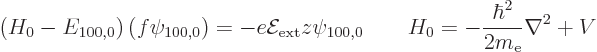
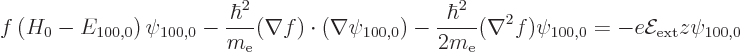
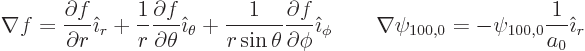
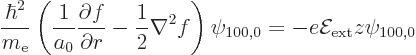
![]()
![]()
![]()
![]() -
-![]()
![]() ,
,![]()
![]() .
.![]()
![]() -
-![]()
![]()