| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
2.5 Eigenvalue Problems
To analyze quantum mechanical systems, it is normally necessary to
find so-called eigenvalues and eigenvectors or eigenfunctions. This
section defines what they are.
A nonzero vector  is called an eigenvector of a matrix
is called an eigenvector of a matrix  if
if
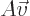 is a multiple of the same vector:
is a multiple of the same vector:
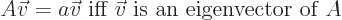 |
(2.13) |
The multiple 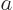 is called the eigenvalue. It is just a number.
is called the eigenvalue. It is just a number.
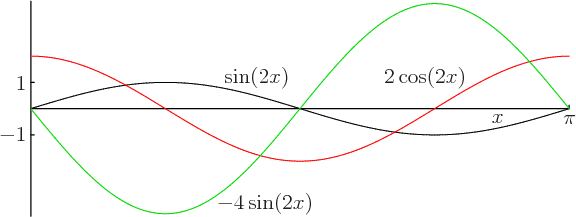
Figure 2.8:
Illustration
of the eigenfunction concept. Function 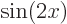 is shown in
black. Its first derivative
is shown in
black. Its first derivative 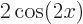 , shown in red, is not
just a multiple of
, shown in red, is not
just a multiple of 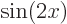 . Therefore
. Therefore 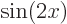 is
not an eigenfunction of the first derivative operator.
However, the second derivative of
is
not an eigenfunction of the first derivative operator.
However, the second derivative of 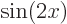 is
is 
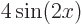 ,
which is shown in green, and that is indeed a multiple of
,
which is shown in green, and that is indeed a multiple of
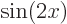 . So
. So 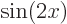 is an eigenfunction of the second
derivative operator, and with eigenvalue
is an eigenfunction of the second
derivative operator, and with eigenvalue  4.
4.
 |
A nonzero function 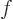 is called an eigenfunction of an operator
is called an eigenfunction of an operator  if
if
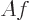 is a multiple of the same function:
is a multiple of the same function:
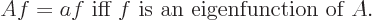 |
(2.14) |
For example, 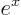 is an eigenfunction of the operator
is an eigenfunction of the operator
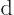

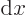 with eigenvalue 1, since
with eigenvalue 1, since 

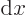
 1
1 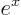 . Another simple example is illustrated in figure
2.8; the function
. Another simple example is illustrated in figure
2.8; the function 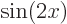 is not an
eigenfunction of the first derivative operator
is not an
eigenfunction of the first derivative operator
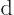

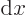 . However it is an eigenfunction of the
second derivative operator
. However it is an eigenfunction of the
second derivative operator 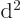

 , and with
eigenvalue
, and with
eigenvalue  4.
4.
Eigenfunctions like 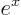 are not very common in quantum mechanics
since they become very large at large
are not very common in quantum mechanics
since they become very large at large  , and that typically
does not describe physical situations. The eigenfunctions of the
first derivative operator
, and that typically
does not describe physical situations. The eigenfunctions of the
first derivative operator 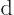

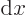 that do appear a lot are of
the form
that do appear a lot are of
the form 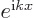 , where
, where 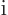

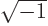 and
and 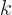 is
an arbitrary real number. The eigenvalue is
is
an arbitrary real number. The eigenvalue is 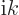 :
:
Function 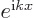 does not blow up at large
does not blow up at large  ; in
particular, the Euler formula (2.5) says:
; in
particular, the Euler formula (2.5) says:
The constant 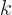 is called the “wave number.”
is called the “wave number.”
Key Points

- If a matrix turns a nonzero vector into a multiple of that
vector, then that vector is an eigenvector of the matrix, and the
multiple is the eigenvalue.

- If an operator turns a nonzero function into a multiple of that
function, then that function is an eigenfunction of the operator,
and the multiple is the eigenvalue.
2.5 Review Questions
-
1.
-
Show that 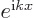 , above, is also an eigenfunction of
, above, is also an eigenfunction of 

 , but with eigenvalue
, but with eigenvalue 
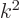 . In fact, it is easy to see that the square of any operator has the same eigenfunctions, but with the square eigenvalues.
. In fact, it is easy to see that the square of any operator has the same eigenfunctions, but with the square eigenvalues.
Solution eigvals-a
-
2.
-
Show that any function of the form 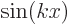 and any function of the form
and any function of the form  , where
, where 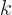 is a constant called the wave number, is an eigenfunction of the operator
is a constant called the wave number, is an eigenfunction of the operator 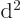

 , though they are not eigenfunctions of
, though they are not eigenfunctions of 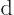

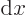 .
.
Solution eigvals-b
-
3.
-
Show that 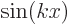 and
and  , with
, with 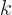 a constant, are eigenfunctions of the inversion operator
a constant, are eigenfunctions of the inversion operator 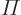 , which turns any function
, which turns any function 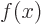 into
into 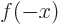 , and find the eigenvalues.
, and find the eigenvalues.
Solution eigvals-c
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() :
:![]() ,
,![]()
![]()
![]() ,
,![]()
![]() .
.![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() .
.![]()
![]() ,
,![]()
![]() ,
,![]()
![]() ,
,