|
|
|
|
|
Next: 2.7 Additional Points |
|
Most operators in quantum mechanics are of a special kind called
Hermitian
. This section lists their most important
properties.
An operator is called Hermitian when it can always be flipped over to
the other side if it appears in a inner product:
| (2.15) |
That is the definition, but Hermitian operators have the following additional special properties:
completeset. This means that any function can be written as some linear combination of the eigenfunctions. (There is a proof in derivation {D.8} for an important example. But see also {N.4}.) In practical terms, it means that you only need to look at the eigenfunctions to completely understand what the operator does.
In the linear algebra of real matrices, Hermitian operators are simply symmetric matrices. A basic example is the inertia matrix of a solid body in Newtonian dynamics. The orthonormal eigenvectors of the inertia matrix give the directions of the principal axes of inertia of the body.
An orthonormal complete set of eigenvectors or eigenfunctions is an
example of a so-called “basis.” In general, a basis is a minimal set of vectors or
functions that you can write all other vectors or functions in terms
of. For example, the unit vectors ![]() ,
,![]() ,
,![]()
The following properties of inner products involving Hermitian operators
are often needed, so they are listed here:
Key Points
- Hermitian operators can be flipped over to the other side in inner products.
- Hermitian operators have only real eigenvalues.
- Hermitian operators have a complete set of orthonormal eigenfunctions (or eigenvectors).
A matrix ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
A matrix ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Show that the operator ![]()
![]()
Generalize the previous question, by showing that any complex constant ![]()
Show that an operator such as ![]() ,
,
Show that the operator ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
periodic
; they must return to the same value at ![]()
![]()
![]()
![]()
![]()
![]() .
.
Show that if ![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
A complete set of orthonormal eigenfunctions of ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
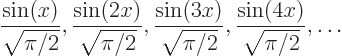
Check that these functions are indeed zero at ![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
Completeness is a much more difficult thing to prove, but they are. The completeness proof in the notes covers this case.
A complete set of orthonormal eigenfunctions of the operator ![]()
![]()
![]()
![]()
![]()
![]()
![]()
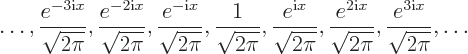
Check that these functions are indeed periodic, orthonormal, and that they are eigenfunctions of ![]()
![]()
![]()
Completeness is a much more difficult thing to prove, but they are. The completeness proof in the notes covers this case.