5.11 Chem­i­cal Bonds

The elec­tron states, or atomic or­bitals, of the el­e­ments dis­cussed in sec­tion 5.9 form the ba­sis for the va­lence bond de­scrip­tion of chem­i­cal bonds. This sec­tion sum­ma­rizes some of the ba­sic ideas in­volved.

5.11.1 Co­va­lent sigma bonds

As pointed out in sec­tion 5.9, he­lium is chem­i­cally in­ert: its out­er­most, and only, shell can hold two elec­trons, and it is full. But hy­dro­gen has only one elec­tron, leav­ing a va­cant po­si­tion for an­other 1s elec­tron. As dis­cussed ear­lier in chap­ter 5.2, two hy­dro­gen atoms are will­ing to share their elec­trons. This gives each atom in some sense two elec­trons in its shell, fill­ing it up. The shared state has lower en­ergy than the two sep­a­rate atoms, so the H$_2$ mol­e­cule stays to­gether. A sketch of the shared 1s elec­trons was given in fig­ure 5.2.

Flu­o­rine has one va­cant spot for an elec­tron in its outer shell just like hy­dro­gen; its outer shell can con­tain 8 elec­trons and flu­o­rine has only seven. One of its 2p states, as­sume it is the hor­i­zon­tal ax­ial state 2p$_z$, has only one elec­tron in it in­stead of two. Two flu­o­rine atoms can share their un­paired elec­trons much like hy­dro­gen atoms do and form an F$_2$ mol­e­cule. This gives each of the two atoms a filled shell. The flu­o­rine mol­e­c­u­lar bond is sketched in fig­ure 5.9 (all other elec­trons have been omit­ted.)

Fig­ure 5.9: Co­va­lent sigma bond con­sist­ing of two 2p$_z$ states.

This bond be­tween p elec­trons looks quite dif­fer­ent from the H$_2$ bond be­tween s elec­trons in fig­ure 5.2, but it is again a co­va­lent one, in which the elec­trons are shared. In ad­di­tion, both bonds are called sigma bonds: if you look at ei­ther bond from the side, it looks ro­ta­tion­ally sym­met­ric, just like an s state. (Sigma is the Greek equiv­a­lent of the let­ter s; it is writ­ten as $\sigma$.)

Key Points

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

Two flu­o­rine or sim­i­lar atoms can share their un­paired 2p elec­trons in much the same way that two hy­dro­gen atoms can share their un­paired 2s elec­trons.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

Since such bonds look like s states when seen from the side, they are called sigma or $\sigma$ bonds.

5.11.2 Co­va­lent pi bonds

The N$_2$ ni­tro­gen mol­e­cule is an­other case of co­va­lent bond­ing. Ni­tro­gen atoms have a to­tal of three un­paired elec­trons, which can be thought of as one each in the 2p$_x$, 2p$_y$, and 2p$_z$ states. Two ni­tro­gen atoms can share their un­paired 2p$_z$ elec­trons in a sigma bond the same way that flu­o­rine does, lon­gi­tu­di­nally.

How­ever, the 2p$_x$ and 2p$_y$ states are nor­mal to the line through the nu­clei; these states must be matched up side­ways. Fig­ure 5.10 il­lus­trates this for the bond be­tween the two ver­ti­cal 2p$_x$ states.

Fig­ure 5.10: Co­va­lent pi bond con­sist­ing of two 2p$_x$ states.

This co­va­lent bond, and the cor­re­spond­ing one be­tween the 2p$_y$ states, looks like a p state when seen from the side, and it is called a pi or $\pi$ bond.

So, the N$_2$ ni­tro­gen mol­e­cule is held to­gether by two pi bonds in ad­di­tion to a sigma bond, mak­ing a triple bond. It is a rel­a­tively in­ert mol­e­cule.

Key Points

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

Un­paired p states can match up side­ways in what are called pi or $\pi$ bonds.

5.11.3 Po­lar co­va­lent bonds and hy­dro­gen bonds

Oxy­gen, lo­cated in be­tween flu­o­rine and ni­tro­gen in the pe­ri­odic ta­ble, has two un­paired elec­trons. It can share these elec­trons with an­other oxy­gen atom to form O$_2$, the mol­e­c­u­lar oxy­gen we breath. How­ever, it can in­stead bind with two hy­dro­gen atoms to form H$_2$O, the wa­ter we drink.

In the wa­ter mol­e­cule, the lone 2p$_z$ elec­tron of oxy­gen is paired with the 1s elec­tron of one hy­dro­gen atom, as shown in fig­ure 5.11.

Fig­ure 5.11: Co­va­lent sigma bond con­sist­ing of a 2p$_z$ and a 1s state.

Sim­i­larly, the lone 2p$_y$ elec­tron is paired with the 1s elec­tron of the other hy­dro­gen atom. Both bonds are sigma bonds: they are lo­cated on the con­nect­ing line be­tween the nu­clei. But in this case each bond con­sists of a 1s and a 2p state, rather than two states of the same type.

Since the $x$ and $y$ axes are or­thog­o­nal, the two hy­dro­gen atoms in wa­ter should be at a 90 de­gree an­gle from each other, rel­a­tive to the oxy­gen nu­cleus. (With­out va­lence bond the­ory, the most log­i­cal guess would surely have been that they would be at op­po­site sides of the oxy­gen atom.) The pre­dicted 90 de­gree an­gle is in fair ap­prox­i­ma­tion to the ex­per­i­men­tal value of 105 de­grees.

The rea­son that the ac­tual an­gle is a bit more may be un­der­stood from the fact that the oxy­gen atom has a higher at­trac­tion for the shared elec­trons, or elec­troneg­a­tiv­ity, than the hy­dro­gen atoms. It will pull the elec­trons partly away from the hy­dro­gen atoms, giv­ing it­self some neg­a­tive charge, and the hy­dro­gen atoms a cor­re­spond­ing pos­i­tive one. The pos­i­tively charged hy­dro­gen atoms re­pel each other, in­creas­ing their an­gle a bit. If you go down one place in the pe­ri­odic ta­ble be­low oxy­gen, to the larger sul­fur atom, H$_2$S has its hy­dro­gen atoms un­der about 93 de­grees, quite close to 90 de­grees.

Bonds like the one in wa­ter, where the neg­a­tive elec­tron charge shifts to­wards the more elec­troneg­a­tive atom, are called po­lar co­va­lent bonds.

It has sig­nif­i­cant con­se­quences for wa­ter, since the pos­i­tively charged hy­dro­gen atoms can elec­tro­sta­t­i­cally at­tract the neg­a­tively charged oxy­gen atoms on other mol­e­cules. This has the ef­fect of cre­at­ing bonds be­tween dif­fer­ent mol­e­cules called “hy­dro­gen bonds.” While much weaker than typ­i­cal co­va­lent bonds, they are strong enough to af­fect the phys­i­cal prop­er­ties of wa­ter. For ex­am­ple, they are the rea­son that wa­ter is nor­mally a liq­uid in­stead of a gas, quite a good idea if you are thirsty, and that ice floats on wa­ter in­stead of sink­ing to the bot­tom of the oceans. Hy­dro­gen is par­tic­u­larly ef­fi­cient at cre­at­ing such bonds be­cause it does not have any other elec­trons to shield its nu­cleus.

Key Points

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

The geom­e­try of the quan­tum states re­flects in the geom­e­try of the formed mol­e­cules.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

When the shar­ing of elec­trons is un­equal, a bond is called po­lar.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

A spe­cial case is hy­dro­gen, which is par­tic­u­larly ef­fec­tive in also cre­at­ing bonds be­tween dif­fer­ent mol­e­cules, hy­dro­gen bonds, when po­lar­ized.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

Hy­dro­gen bonds give wa­ter un­usual prop­er­ties that are crit­i­cal for life on earth.

5.11.4 Pro­mo­tion and hy­bridiza­tion

While va­lence bond the­ory man­aged to ex­plain a num­ber of chem­i­cal bonds so far, two im­por­tant ad­di­tional in­gre­di­ents need to be added. Oth­er­wise it will not at all be able to ex­plain or­ganic chem­istry, the chem­istry of car­bon crit­i­cal to life.

Car­bon has two un­paired 2p elec­trons just like oxy­gen does; the dif­fer­ence be­tween the atoms is that oxy­gen has in ad­di­tion two paired 2p elec­trons. With two un­paired elec­trons, it might seem that car­bon should form two bonds like oxy­gen.

But that is not what hap­pens; nor­mally car­bon forms four bonds in­stead of two. In chem­i­cal bonds, one of car­bon's paired 2s elec­trons moves to the empty 2p state, leav­ing car­bon with four un­paired elec­trons. It is said that the 2s elec­tron is pro­moted to the 2p state. This re­quires en­ergy, but the en­ergy gained by hav­ing four bonds more than makes up for it.

Pro­mo­tion ex­plains why a mol­e­cule such as CH$_4$ forms. In­clud­ing the 4 shared hy­dro­gen elec­trons, the car­bon atom has 8 elec­trons in its outer shell, so its shell is full. It has made as many bonds as it can sup­port.

How­ever, pro­mo­tion is still not enough to ex­plain the mol­e­cule. If the CH$_4$ mol­e­cule was merely a mat­ter of pro­mot­ing one of the 2s elec­trons into the va­cant 2p$_y$ state, the mol­e­cule should have three hy­dro­gen atoms un­der 90 de­grees, shar­ing the 2p$_x$, 2p$_y$, and 2p$_z$ elec­trons re­spec­tively, and one hy­dro­gen atom else­where, shar­ing the re­main­ing 2s elec­tron. In re­al­ity, the CH$_4$ mol­e­cule is shaped like a reg­u­lar tetra­he­dron, with an­gles of 109.5 de­grees be­tween all four hy­dro­gens.

The ex­pla­na­tion is that, rather than us­ing the 2p$_x$, 2p$_y$, 2p$_z$, and 2s states di­rectly, the car­bon atom forms new com­bi­na­tions of the four called hy­brid states. (This is not un­like how the torus-shaped $\psi_{211}$ and $\psi_{21-1}$ states were re­com­bined in chap­ter 4.3 to pro­duce the equiv­a­lent 2p$_x$ and 2p$_y$ pointer states.)

In case of CH$_4$, the car­bon con­verts the 2s, 2p$_x$, 2p$_y$, and 2p$_z$ states into four new states. These are called sp$\POW9,{3}$ states, since they are formed from one s and three p states. They are given by:

$$\renewedcommand{arraystretch}{1.8} \begin{array}{l} \vert... ...e-\vert\mbox{2p}_y\rangle+\vert\mbox{2p}_z\rangle) \end{array}$$

where the kets de­note the wave func­tions of the in­di­cated states.

All four sp$\POW9,{3}$ hy­brids have the same shape, shown in fig­ure 5.12.

Fig­ure 5.12: Shape of an sp$\POW9,{3}$ hy­brid state.

The asym­met­ri­cal shape can in­crease the over­lap be­tween the wave func­tions in the bond. The four sp$\POW9,{3}$ hy­brids are un­der equal 109.5 de­grees an­gles from each other, pro­duc­ing the tetra­he­dral struc­ture of the CH$_4$ mol­e­cule. And of di­a­mond, for that mat­ter. With the atoms bound to­gether in all spa­tial di­rec­tions, di­a­mond is an ex­tremely hard ma­te­r­ial.

But car­bon is a very ver­sa­tile atom. In graphite, and car­bon nan­otubes, car­bon atoms arrange them­selves in lay­ers in­stead of three-di­men­sion­al struc­tures. Car­bon achieves this trick by leav­ing the 2p-state in the di­rec­tion nor­mal to the plane, call it p$_x$, out of the hy­bridiza­tion. The two 2p states in the plane plus the 2s state can then be com­bined into three sp$\POW9,{2}$ states:

$$\renewedcommand{arraystretch}{2.3} \begin{array}{l} \vert... ...splaystyle\frac{1}{\sqrt2}}\vert\mbox{2p}_y\rangle \end{array}$$

Each is shaped as shown in fig­ure 5.13.

Fig­ure 5.13: Shapes of the sp$\POW9,{2}$ (left) and sp (right) hy­brids.

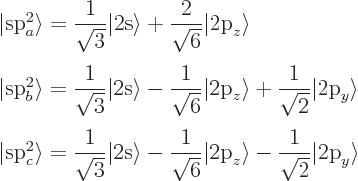
These pla­nar hy­brids are un­der 120 de­gree an­gles from each other, giv­ing graphite its hexag­o­nal struc­ture. The left-out p elec­trons nor­mal to the plane can form pi bonds with each other. A pla­nar mol­e­cule formed us­ing sp$\POW9,{2}$ hy­bridiza­tion is eth­yl­ene (C$_2$H$_4$); it has all six nu­clei in the same plane. The pi bond nor­mal to the plane pre­vents out-of-plane ro­ta­tion of the nu­clei around the line con­nect­ing the car­bons, keep­ing the plane rigid.

Fi­nally, car­bon can com­bine the 2s state with a sin­gle 2p state to form two sp hy­brids un­der 180 de­grees from each other:

$$\renewedcommand{arraystretch}{2.3} \begin{array}{l} \vert... ...2}}(\vert\mbox{2s}\rangle-\vert\mbox{2p}_z\rangle) \end{array}$$

An ex­am­ple sp hy­bridiza­tion is acety­lene, (C$_2$H$_2$), which has all its four nu­clei on a sin­gle line.

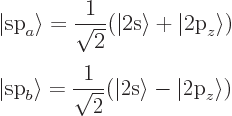
Key Points

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

The chem­istry of car­bon is crit­i­cal for life as we know it.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

It in­volves two ad­di­tional ideas; one is pro­mo­tion, where car­bon kicks one of its 2s elec­trons into a 2p state. This gives car­bon one 2s and three 2p elec­trons.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

The sec­ond idea is hy­bridiza­tion, where car­bon com­bines these four states in cre­ative new com­bi­na­tions called hy­brids.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

In sp$\POW9,{3}$ hy­bridiza­tion, car­bon cre­ates four hy­brids in a reg­u­lar tetra­he­dron com­bi­na­tion.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

In sp$\POW9,{2}$ hy­bridiza­tion, car­bon cre­ates three hy­brids in a plane, spaced at 120 de­gree in­ter­vals. That leaves a con­ven­tional 2p state in the di­rec­tion nor­mal to the plane.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

In sp hy­bridiza­tion, car­bon cre­ates two hy­brids along a line, point­ing in op­po­site di­rec­tions. That leaves two con­ven­tional 2p states nor­mal to the line of the hy­brids and to each other.

5.11.5 Ionic bonds

Ionic bonds are the ex­treme po­lar bonds; they oc­cur if there is a big dif­fer­ence be­tween the elec­troneg­a­tiv­i­ties of the atoms in­volved.

An ex­am­ple is kitchen salt, NaCl. The sodium atom has only one elec­tron in its outer shell, a loosely bound 3s one. The chlo­rine has seven elec­trons in its outer shell and needs only one more to fill it. When the two re­act, the chlo­rine does not just share the lone elec­tron of the sodium atom, it sim­ply takes it away. It makes the chlo­rine a neg­a­tively charged ion. Sim­i­larly, it leaves the sodium as a pos­i­tively charged ion.

The charged ions are bound to­gether by elec­tro­sta­tic forces. Since these forces act in all di­rec­tions, each ion does not just at­tract the op­po­site ion it ex­changed the elec­tron with, but all sur­round­ing op­po­site ions. And since in salt each sodium ion is sur­rounded by six chlo­rine ions and vice versa, the num­ber of bonds that ex­ists is large.

Since so many bonds must be bro­ken to take a ionic sub­stance apart, their prop­er­ties are quite dif­fer­ent from co­va­lently bounded sub­stances. For ex­am­ple, salt is a solid with a high melt­ing point, while the co­va­lently bounded Cl$_2$ chlo­rine mol­e­cule is nor­mally a gas, since the bonds be­tween dif­fer­ent mol­e­cules are weak. In­deed, the co­va­lently bound hy­dro­gen mol­e­cule that has been dis­cussed much in this chap­ter re­mains a gas un­til es­pe­cially low cryo­genic tem­per­a­tures.

Chap­ter 10.2 will give a more quan­ti­ta­tive dis­cus­sion of ionic mol­e­cules and solids.

Key Points

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

When a bond is so po­lar that prac­ti­cally speak­ing one atom takes the elec­tron away from the other, the bond is called ionic.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

Ionic sub­stances like salt tend to form strong solids, un­like typ­i­cal purely co­va­lently bound mol­e­cules like hy­dro­gen that tend to form gases.

5.11.6 Lim­i­ta­tions of va­lence bond the­ory

Va­lence bond the­ory does a ter­rific job of de­scrib­ing chem­i­cal bonds, pro­duc­ing a lot of es­sen­tially cor­rect, and very non­triv­ial pre­dic­tions, but it does have lim­i­ta­tions.

One place it fails is for the O$_2$ oxy­gen mol­e­cule. In the mol­e­cule, the atoms share their un­paired 2p$_x$ and 2p$_z$ elec­trons. With all elec­trons sym­met­ri­cally paired in the spa­tial states, the elec­trons should all be in sin­glet spin states hav­ing no net spin. How­ever, it turns out that oxy­gen is strongly para­mag­netic, in­di­cat­ing that there is in fact net spin. The prob­lem in va­lence bond the­ory that causes this er­ror is that it ig­nores the al­ready paired-up elec­trons in the 2p$_y$ states. In the mol­e­cule, the filled 2p$_y$ states of the atoms are next to each other and they do in­ter­act. In par­tic­u­lar, one of the to­tal of four 2p$_y$ elec­trons jumps over to the 2p$_x$ states, where it only ex­pe­ri­ences re­pul­sion by two other elec­trons in­stead of by three. The spa­tial state of the elec­tron that jumps over is no longer equal to that of its twin, al­low­ing them to have equal in­stead of op­po­site spin.

Va­lence bond the­ory also has prob­lems with sin­gle-elec­tron bonds such as the hy­dro­gen mol­e­c­u­lar ion, or with ben­zene, in which the car­bon atoms are held to­gether with what is es­sen­tially 1.5 bonds, or rather, bonds shared as in a two state sys­tem. Ex­cited states pro­duce ma­jor dif­fi­cul­ties. Var­i­ous fixes and im­proved the­o­ries ex­ist.

Key Points

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

Va­lence bond the­ory is ex­tremely use­ful. It is con­cep­tu­ally sim­ple and ex­plains much of the most im­por­tant chem­i­cal bonds.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

How­ever, it does have def­i­nite lim­i­ta­tions: some types of bonds are not cor­rectly or not at all de­scribed by it.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

Lit­tle in life is ideal, isn’t it?