|
|
|
|
|
Next: 10.3 Metals |
|
A typical example of a ionic solid is ordinary salt, NaCl. There is little quantitative quantum mechanics required to describe either the salt molecule or solid salt. Still, there are some important qualitative points, so it seems useful to include a discussion in this book. Both molecule and solid will be described in this subsection, since the ideas are very similar.
To form a NaCl salt molecule, a clorine atom takes the loosely bound lone 3s electron away from a natrium (sodium) atom and puts it in its single still vacant 3p position. That leaves a negative chlorine ion with filled K, L, and M shells and a positive natrium ion with just filled K and L shells. Since the combined electron distribution of filled shells is spherically symmetric, you can reasonably think of the two ions as somewhat soft billiard balls. Since they have opposite charge, they stick together into a salt molecule as sketched in figure 10.1. The natrium ion is a bit less than two Å in diameter, the clorine one a bit less than four.
The energetics of this process is rather interesting. Assume that you start out with a neutral natrium atom and a neutral chlorine atom that are far apart. To take the lone 2s electron out of the natrium atom, and leave it at rest at a position far from either the natrium or the chlorine atom, takes an amount of energy called the “ionization energy” of natrium. Its value is 5.14 eV (electron volts).
To take that free electron at rest and put it into the vacant 3p position of the chlorine ion gives back an amount of energy called the “electron affinity” of clorine. Its value is 3.62 eV.
(Electron affinity, the willingness to take on free electrons, is not to be confused with “electronegativity,” the willingness to take on electrons in chemical bonds. Unlike electronegativity, electron affinity varies wildly from element to element in the periodic table. There is some system in it, still, especially within single columns. It may also be noted that there seems to be some disagreement about the definition of electronegativity, in particular for atoms or molecules that cannot stably bind a free electron, {N.19}.)
Anyway, since it takes 5.14 eV to take the electron out of natrium, and you get only 3.62 eV back by putting it into clorine, you may wonder how a salt molecule could ever be stable. But the described picture is very misleading. It does not really take 5.14 eV to take the electron out of natrium; most of that energy is used to pull the liberated electron and positive ion far apart. In the NaCl molecule, they are not pulled far apart; the positive natrium ion and negative chlorine ion stick together as in figure 10.1.
In other words, to create the widely separated positive natrium ion
and negative chlorine ion took ![]()
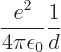
There are a few reasons why it is slightly off, but one is that the Coulomb expression above is only correct if the ions were billiard balls that would move unimpeded towards each other until they hit. Actually, the atoms are somewhat softer than billiard balls; their mutual repulsion force ramps up quickly, but not instantaneously. That means that the repulsion force will do a small amount of negative work during the final part of the approach of the ions. Also, the uncertainty principle does not allow the localized ions to have exactly zero kinetic energy. But as you see, these are small effects. It may also be noted that the repulsion between the ions is mostly Pauli repulsion, as described in section 5.10.
Now the electrostatic force that keeps the two ions together in the molecule is omni-directional. That means that if you bring a lot of salt molecules together, the clorine ions will also attract the natrium ions of other molecules and vice versa. As a result, under normal conditions, salt molecules pack together into solid salt crystals, as shown in figure 10.2. The ions arrange themselves very neatly into a pattern that allows each ion to be surrounded by as many attracting ions of the opposite kind as possible. In fact, as figure 10.2 indicates, each ion is surrounded by six ions of the opposite kind: four in the same vertical plane, a fifth behind it, and a sixth in front of it. A more detailed description of the crystal structure will be given next, but first consider what it means for the energy.
Since when the molecules pack into a solid, each ion gets next to six
ions of the opposite type, the simplest guess would be that the 6.1 eV
Coulomb attraction of the ions in the molecule would increase by a
factor 6 in the solid. But that is a bad approximation: in the solid,
each ion is not just surrounded by six attracting ions of the opposite
kind, but also by twelve repelling ions of the same kind that are only
slightly further away, then again eight attracting ions still a bit
further away, etcetera. The net effect is that the Coulomb attraction
is only 1.75 times higher in the solid than the lone molecules would
have. The factor 1.75 is called the “Madelung constant. So, all else being the same, by forming a salt
crystal the salt molecules would raise their Coulomb attraction to
![]()
That is still not quite right, because in the solid, the ions are
farther apart than in the molecule. Recall that in the solid, each
attracting ion is surrounded by repelling ions of the opposite kind,
reducing the attraction between pairs. In the solid, opposite ions
are 2.82 Å apart instead of 2.36, so the Coulomb energy reduces to
10.7 ![]()
![]() C
C![]() C
C
Finally, consider the crystal structure that the molecules combine into. One way of thinking of it is as a three-dimensional chess board structure. In figure 10.2, think of the frontal plane as a chess board of black and white cubes, with a natrium nucleus in the center of each white cube and a clorine nucleus in the center of each black one. The next plane of atoms can similarly be considered to consists of black and white cubes, where the back cubes are behind the white cubes of the frontal plane and vice-versa. And the same way for further planes.
However, this is not how a material scientist would think about the structure. A material scientist likes to describe a crystal in terms copies of a simple unit, called the “basis,” that are stacked together in a regular manner. One possible choice for the basis in salt is a single natrium ion plus a single clorine ion to the right of it, like the molecule of figure 10.1. In figure 10.3 the ions of the salt crystal have been moved far apart to make the actual structure visible, and the two atoms of the basis units have been joined by a blue line. Note that the entire structure consists of these basis units.
But also note that the molecules lose their identity in a ionic solid.
You could just as well build up the crystal from vertical
molecules,
say, instead of horizontal ones. In fact,
there are six reasonable choices of basis, depending on which of its
six surrounding chlorine ions you want to associate each natrium ion
with. There are of course always countless unreasonable ones...
The regular way in which the bases are stacked together to form the complete crystal structure is called the “lattice.” You can think of the volume of the salt crystal as consisting of little cubes called “unit cells” indicated by the red frames in figure 10.3. There are clorine atoms at the corners of the cubes as well as at the center points of the faces of the cubes. That is the reason the salt lattice is called the “face centered cubic” (FCC) lattice. Also note that if you shift the unit cells half a cell to the left, it will be the natrium ions that are at the corners and face centers of the cubes. In general, every point of a basis is arranged in the crystal according to the same lattice.
You will agree that it sounds much more professional to say that you have studied the face-centered cubic arrangement of the basis in a NaCl crystal than to say that you have studied the three-dimensional chess board structure of salt.
Key Points
- In a fully ionic bond like NaCl, one atom takes an electron away from another.
- The positive and negative ions stick together by electrostatic force, creating a molecule.
- Because of the same electrostatic force, molecules clump together into strong ionic solids.
- The crystal structure of NaCl consists of copies of a two-atom NaCL basis arranged in a face-centered cubic lattice.