|
|
|
|
|
Next: 14.6 Draft: Mass and energy |
|
Nuclear decay is governed by chance. It is impossible to tell exactly when any specific nucleus will decay. Therefore, the decay is phrased in terms of statistical quantities like specific decay rate, lifetime and half-life. This section explains how these are defined.
As a generic example of an unstable nucleus, consider tritium, an
isotope of hydrogen. The ![]()
![]()
helion.
The original
triton is lost.
Unlike the normal
![]()
(Note that the triton decays even though it has two neutrons, a magic number. But the helion it decays to has two protons, also magic. And just like a lone neutron decays into a less heavy proton, two neutrons in the tiny triton is just too much of a neutron excess compared to the negligible additional Coulomb repulsion in the helion.)
The big question in this section is, when will an unstable nucleus like the triton decay? Unfortunately, there is no complete anwer to that question. A given triton might last for 10 years, or it might last for 20 years or whatever. It could last less than a year, though that is not very likely. It could last for 100 years, even though that is much less likely still. But there is no way to tell for sure.
However, suppose you take a very large number of tritons and record
for each how long the triton lives. Then you can average all these
times and you get a number that is called the “lifetime” ![]()
If you average over enough tritons, you will find this mean lifetime of tritons to be almost 18 years. But not a single triton will decay after exactly 18 years. It is much like the expected lifetime of a newborn baby in the USA is, say, 80 years. Despite that, almost no one dies on their 80th birthday. Some die at birth or as kids.
Still, there is one big difference between people and nuclei. If you
have a person who is 80 years old, surely you do not expect them to
live until they become 160 years old. But if you have a bunch of
tritons, on average this bunch of tritons will last for another 18
years. That is regardless of how long these tritons have survived
already when you start observing them. Nuclear decay is a completely
random process that occurs out of the blue;
it does
not depend on any previous history of the nucleus.
There is another issue. Unless you are an accountant by calling, why would you want to sit down, measure lifetimes of nuclei, and average them? What is the use?
A physically much more relevant scenario is that you have managed to
create a large number of tritons, and you would like to know how long
they will last for doing experiments. In particular, you might want
to know how long it takes before half of the tritons you created with
blood, tears, and tax-payer money, are gone. This physically more
meaningful time period is called the half-life
![]() .
.![]() :
:
| (14.3) |
The half-life of the triton is 12.32 years. So if you initially have
a large collection of tritium nuclei, after 12.32 years only half will
be left. After 24.64 years, only a quarter will remain, and after a
century only 0.4%. After a millennium only 4 1![]()
![]()
Now the earth is over 4 million millenia old. So you will appreciate that almost none of the tritium ever present on earth still exists. Some new tritium is continuously being created in the atmosphere by high-energy cosmic rays, but because of the geologically short half-life, there is no measurable accumulation. The total amount of tritium present on earth is virtually zero.
As in an earlier section, figure 14.3 shows again the decay processes of the nuclei. But unlike in the earlier figure 14.2, this time the square size of each nucleus has been adjusted to illustrate its half-life.
For the full size squares in the figure, the half-life is 1![]()
![]()
On the other hand, if the square size of a nucleus is even
slightly smaller than full size, then most of these nuclei that
the universe ever created will have decayed. You may note that the
square size of the ![]()
On the other hand, all stable green nuclei have full size squares.
You might also note bismuth-209, ![]() .
.![]()
![]()
Based on various arguments, it was decided to take the minimum
half-life shown in figure 14.3 to be one nanosecond.
Clearly the figure needs some lower limit. And a nanosecond
is really fast for alpha decay, and much faster than any beta decay.
(Note that you do not see any really small red or blue squares in
figure 14.3, and only a few yellow ones.) And for
gamma decay, a nanosecond is often used as a cut-off between
prompt” and “isomeric
decay.
Still, some nuclear decay processes are much quicker than a
nanosecond. For example, you might note that the light nuclei that
decay though proton or neutron emission in figure 14.2
have disappeared in figure 14.3. Such a decay process
may have a half life on the order of 100 ys, (i.e. 100 1![]()
move
just once through a nucleus with a size of the
order of femtometers.
Another notable nucleus that has disappeared is
![]() ,
,![]() ,
,![]()
Besides (mean) lifetime and half-life, there is one more related term
that is commonly used in describing nuclear decays. It is called the
“specific decay rate” ![]() .
.![]() :
:
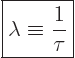 |
(14.4) |
To better understand the various variables mathematically, it may be
worthwhile to see how the mentioned relationships between them arise.
First, according to the very definition of the decay rate ![]()
![]() ,
,![]() ,
,![]()
| (14.5) |
| (14.6) |

One very important point must be emphasized. Many nuclei undergo more than one decay process. In that case, each decay process has its own decay rate, independent of the other decay processes. In such cases,
Always add specific decay rates, never lifetimes or half-lifes.The sum of the specific decay rates gives the total specific decay rate of the nucleus. The reciprocal of that total is the actual lifetime. Multiply by
You probably think that having three different names, the specific
decay rate ![]() ,
,![]() ,
,![]() ,
,constant
is a much more vague term,
maximizing confusion. Even better, how does “disintegration constant” sound? Especially since the nucleus
clearly does not disintegrate in decays other than spontaneous
fission? Why not call it “specific activity,”come to think of it? Activity is another of these vague terms that
the hated nonspecialists cannot make heads or tails of.
How about calling the product ![]()
You probably want some units to go with that! What is more logical
than to take the decay rate or activity to be in units of “curie,” with symbol Ci and equal 3.7 1![]()
Of course the activity
only tells you the amount of
decays, not how bad the generated radiation is for your health. The
“exposure” is the ionization produced by the radiation in a
given mass of air, in SI units of Coulomb per kg. Exposure is very
important for all people made of air. Of course, a better unit than a
blasted SI one is needed, so the “roentgen” or “röntgen” R is defined to 2.58 1![]()
But health-wise you may be more interested in the “absorbed dose” or “total ionizing dose” or “TID.” That is the radiation energy absorbed per unit mass. That would be in J/kg or “gray,” Gy, in SI units, but people really use the “rad” which is one hundredth of a gray.
If an organ or tissue absorbs a given dose of radiation, it is likely
to be a lot worse if all that radiation is concentrated near the
surface than if it is spread out. The “quality factor” ![]()
![]()
The bad effects of the radiation on your health are taken to be approximately given by the “equivalent dose,” equal to the average absorbed dose of the organ or tissue times the radiation weighting factor. It is in SI units of J/kg, called the “sievert” Sv, but people really use the “rem,” equal to one hundredth of a sievert. Note that the units of dose and equivalent dose are equal; the name is just a way to indicate what quantity you are talking about. It works if you can remember all these names.
To get the “effective dose” for your complete body, the equivalent doses for the organs and tissues must still be multiplied by “tissue weighting factors and summed. The weighting factors add up to one when summed over all the parts of your body. The ICRP defines “dose equivalent” different from equivalent dose. Dose equivalent is used on an operational basis. The personal dose equivalent is defined as the product of the dose at a point at an appropriate depth in tissue, (usually below the point where the dosimeter is worn), times the quality factor (not the radiation weighting factor).