| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.56 Number of system eigenfunctions
This note derives the number of energy eigenfunctions 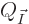 for a given set
for a given set 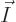

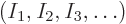 of shelf
occupation numbers,
of shelf
occupation numbers, 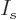 being the number of particles on shelf
number
being the number of particles on shelf
number 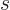 . The number of single-particle eigenfunctions on
shelf number
. The number of single-particle eigenfunctions on
shelf number 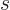 is indicated by
is indicated by 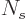 .
.
Consider first the case of distinguishable particles, referring to
figure 11.1 for an example. The question is how many
different eigenfunctions can be created with the given shelf numbers.
What are the ways to create different ones? Well, the first choice
that can be made is what are the 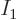 particles that go on shelf
1. If you pick out
particles that go on shelf
1. If you pick out 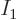 particles from the
particles from the 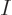 total particles, you
have
total particles, you
have 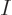 choices for particle 1, next there are
choices for particle 1, next there are 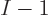 choices left for
particle 2, then
choices left for
particle 2, then 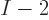 for particle 3. The total number of possible
ways of choosing the
for particle 3. The total number of possible
ways of choosing the 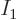 particles is then
particles is then
However, this overestimates the number of variations in eigenfunctions
that you can create by selecting the 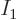 particles: the only thing
that makes a difference for the eigenfunctions is what
particles you pick to go on shelf 1; the order in which you
chose to pick them out of the total set of
particles: the only thing
that makes a difference for the eigenfunctions is what
particles you pick to go on shelf 1; the order in which you
chose to pick them out of the total set of 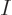 makes no difference.
If you chose a set of
makes no difference.
If you chose a set of 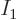 particles in an arbitrary order, you get
no difference in eigenfunction compared to the case that you pick out
the same particles sorted by number. To correct for this, the number
of eigenfunction variations above must be divided by the number of
different orderings in which a set of
particles in an arbitrary order, you get
no difference in eigenfunction compared to the case that you pick out
the same particles sorted by number. To correct for this, the number
of eigenfunction variations above must be divided by the number of
different orderings in which a set of 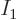 particles can come out of
the total collection. That will give the number of different
sets of particles, sorted by number, that can be selected. The
number of ways that a set of
particles can come out of
the total collection. That will give the number of different
sets of particles, sorted by number, that can be selected. The
number of ways that a set of 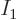 particles can be ordered is
particles can be ordered is
there are 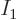 possibilities for the particle that comes first in the
sorted set, then
possibilities for the particle that comes first in the
sorted set, then 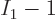 possibilities left for the particle that
comes second, etcetera. Dividing the earlier expression by
possibilities left for the particle that
comes second, etcetera. Dividing the earlier expression by
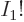 , the number of different sets of
, the number of different sets of 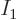 particles that can
be selected for shelf 1 becomes
particles that can
be selected for shelf 1 becomes
But further variations in eigenfunctions are still possible in the way
these 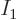 particles are distributed over the
particles are distributed over the 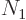 single-particle
states on shelf 1. There are
single-particle
states on shelf 1. There are 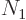 possible single-particle states
for the first particle of the sorted set, times
possible single-particle states
for the first particle of the sorted set, times 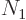 possible
single-particle states for the second particle, etcetera, making a
total of
possible
single-particle states for the second particle, etcetera, making a
total of 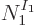 variations. That number of variations exists for
each of the individual sorted sets of particles, so the total number
of variations in eigenfunctions is the product:
variations. That number of variations exists for
each of the individual sorted sets of particles, so the total number
of variations in eigenfunctions is the product:
This can be written more concisely by noting that the bottom of the
fraction is per definition 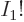 while the top equals
while the top equals
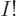
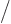
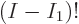 : note that the terms missing from
: note that the terms missing from 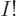 in the
top are exactly
in the
top are exactly 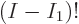 . (In the special case that
. (In the special case that 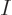

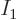 , all particles on shelf 1, this still works since
mathematics defines 0! = 1.) So, the number of variations in
eigenfunctions so far is:
, all particles on shelf 1, this still works since
mathematics defines 0! = 1.) So, the number of variations in
eigenfunctions so far is:
The fraction is known in mathematics as “I choose
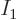 .”
.”
Further variations in eigenfunctions are possible in the way that the
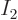 particles on shelf 2 are chosen and distributed over the
single-particle states on that shelf. The analysis is just like the
one for shelf 1, except that shelf 1 has left only
particles on shelf 2 are chosen and distributed over the
single-particle states on that shelf. The analysis is just like the
one for shelf 1, except that shelf 1 has left only 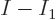 particles
for shelf 2 to chose from. So the number of additional variations
related to shelf 2 becomes
particles
for shelf 2 to chose from. So the number of additional variations
related to shelf 2 becomes
The same way the number of eigenfunction variations for shelves 3, 4, ...
can be found, and the grand total of different eigenfunctions is
This terminates at the shelf number 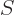 beyond which there are no more
particles left, when
beyond which there are no more
particles left, when 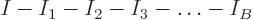
 0. All further
shelves will be empty. Empty shelves might just as well not exist,
they do not change the eigenfunction count. Fortunately, there is no
need to exclude empty shelves from the mathematical expression above,
it can be used either way. For example, if shelf 2 would be empty,
e.g.
0. All further
shelves will be empty. Empty shelves might just as well not exist,
they do not change the eigenfunction count. Fortunately, there is no
need to exclude empty shelves from the mathematical expression above,
it can be used either way. For example, if shelf 2 would be empty,
e.g. 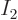
 0, then
0, then 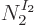
 1 and
1 and 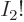
 1, and
the factors
1, and
the factors 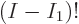 and
and 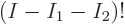 cancel each other. So the
factor due to empty shelf 2 becomes multiplying by one, it does not
change the eigenfunction count.
cancel each other. So the
factor due to empty shelf 2 becomes multiplying by one, it does not
change the eigenfunction count.
Note that various factors cancel in the eigenfunction count above, it
simplifies to the final expression
Mathematicians like to symbolically write a product of indexed factors
like this using the product symbol 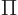 :
:
It means exactly the same as the written-out product.
Next the eigenfunction count for fermions. Refer now to figure
11.3. For any shelf 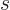 , it is given that there
are
, it is given that there
are 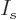 particles on that shelf, and the only variations in
eigenfunctions that can be achieved are in the way that these
particles are distributed over the
particles on that shelf, and the only variations in
eigenfunctions that can be achieved are in the way that these
particles are distributed over the 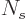 single-particle
eigenfunctions on that shelf. The fermions are identical, but to
simplify the reasoning, for now assume that you stamp numbers on them
from 1 to
single-particle
eigenfunctions on that shelf. The fermions are identical, but to
simplify the reasoning, for now assume that you stamp numbers on them
from 1 to 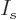 . Then fermion 1 can go into
. Then fermion 1 can go into 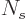 single-particle states, leaving
single-particle states, leaving 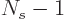 states that fermion 2 can go
into, then
states that fermion 2 can go
into, then 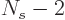 states that fermion 3 can go into, etcetera. That
produces a total of
states that fermion 3 can go into, etcetera. That
produces a total of
variations. But most of these differ only in the order of the numbers
stamped on the fermions; differences in the numbers stamped on the
electrons do not constitute a difference in eigenfunction. The only
difference is in whether a state is occupied by a fermion or not, not
what number is stamped on it. Since, as explained under
distinguishable particles, the number of ways 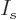 particles can be
ordered is
particles can be
ordered is 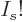 , it follows that the formula above over-counts
the number of variations in eigenfunctions by that factor. To
correct, divide by
, it follows that the formula above over-counts
the number of variations in eigenfunctions by that factor. To
correct, divide by 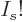 , giving the number of variations as
, giving the number of variations as
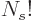
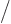
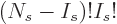 , or “
, or “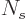 choose
choose
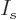 .” The combined number of variations in
eigenfunctions for all shelves then becomes
.” The combined number of variations in
eigenfunctions for all shelves then becomes
If a shelf is empty, it makes again no difference; the corresponding
factor is again one. But another restriction applies for fermions:
there should not be any eigenfunctions if any shelf number 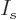 is
greater than the number of states
is
greater than the number of states 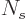 on that shelf. There can be
at most one particle in each state. Fortunately, mathematics defines
factorials of negative integer numbers to be infinite, and the infinite
factor
on that shelf. There can be
at most one particle in each state. Fortunately, mathematics defines
factorials of negative integer numbers to be infinite, and the infinite
factor 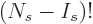 in the bottom will turn the eigenfunction count
into zero as it should. The formula can be used whatever the shelf
numbers are.
in the bottom will turn the eigenfunction count
into zero as it should. The formula can be used whatever the shelf
numbers are.
Figure D.3:
Schematic of an example boson distribution on a shelf.
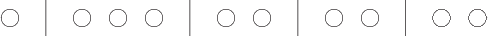 |
Last but not least, the eigenfunction count for bosons. Refer now to
figure 11.2. This one is tricky, but a trick solves it.
To illustrate the idea, take shelf 2 in figure 11.2 as an
example. It is reproduced in condensed form in figure
D.3. The figure merely shows the particles and the
lines separating the single-particle states. Like for the fermions,
the question is, how many ways can the 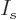 bosons be arranged inside
the
bosons be arranged inside
the 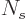 single-particle states? In other words, how many variations
are there on a schematic like the one shown in figure
D.3? To figure it out, stamp identifying numbers on
all the elements, particles and single-state separating lines alike,
ranging from 1 to
single-particle states? In other words, how many variations
are there on a schematic like the one shown in figure
D.3? To figure it out, stamp identifying numbers on
all the elements, particles and single-state separating lines alike,
ranging from 1 to 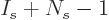 . Following the same reasoning as
before, there are
. Following the same reasoning as
before, there are 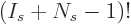 different ways to order these
numbered objects. As before, now back off. All the different
orderings of the numbers stamped on the bosons,
different ways to order these
numbered objects. As before, now back off. All the different
orderings of the numbers stamped on the bosons, 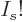 of them,
produce no difference in eigenfunction, so divide by
of them,
produce no difference in eigenfunction, so divide by 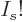 to fix it
up. Similarly, all the different orderings of the single-particle
state boundaries produce no difference in eigenfunction, so divide by
to fix it
up. Similarly, all the different orderings of the single-particle
state boundaries produce no difference in eigenfunction, so divide by
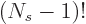 . The number of variations in eigenfunctions possible
by rearranging the particles on a single shelf
. The number of variations in eigenfunctions possible
by rearranging the particles on a single shelf 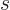 is then
is then
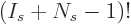
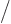
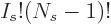 . The total for all shelves is
. The total for all shelves is
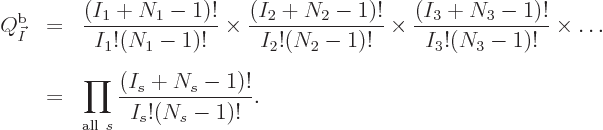
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
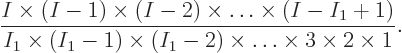
![]()
![]()
![]()
![]()
![]()
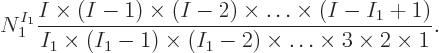
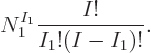
![]()
![]()
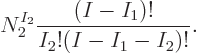
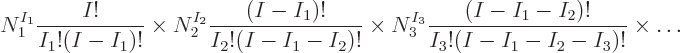
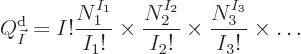
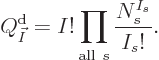
![]() ,
,![]()
![]()
![]() .
.![]()
![]()
![]()
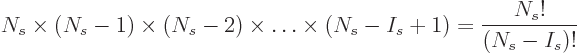
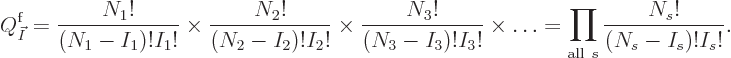
![]()
![]()
![]() .
.![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]() .
.