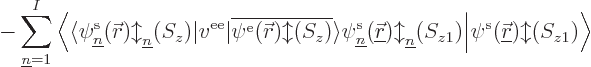| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.55 Why the Fock operator is Hermitian
To verify that the Fock operator is Hermitian, first note that 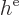 is Hermitian since it is an Hamiltonian. Next if you form the inner
product
is Hermitian since it is an Hamiltonian. Next if you form the inner
product
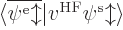 , the
first term in
, the
first term in 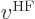 , the Coulomb term, can be taken to
the other side since it is just a real function. The second term, the
exchange one, produces the inner product,
, the Coulomb term, can be taken to
the other side since it is just a real function. The second term, the
exchange one, produces the inner product,
and if you take the operator to the other side, you get
and writing out these inner products as six-dimensional spatial
integrals and sums over spin, you see that they are the same.
![]()
![]() ,
,![]() ,
,