|
|
|
|
|
Next: D.24 Hydrogen molecule ground state and spin |
|
To find the approximate solution for the hydrogen molecule, the key is
to be able to find the expectation energy of the approximate wave
functions
![]() .
.
First, for given ![]()
![]()
![]() ,
,![]()
![]()
| (D.11) |
The inner product
![\begin{displaymath}
\left\langle{E}\right\rangle = 2 E_1 - {\displaystyle\frac{...
...ab\langle\psi_{\rm {l}}\vert\psi_{\rm {r}}\rangle^2 A_2\Biggr]
\end{displaymath}](img6319.gif)
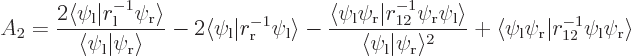
In any case, the basic idea is still to print out expectation
energies, easy to obtain or not, and to examine the print-out to see
at what values of ![]()
![]()
![]()
![]()
The results are listed in the main text, but here are some more data
that may be of interest. At the 1.62 ![]()
![]()
![]()
![]()
![]()
![]() 1
1
The nucleus to electron attraction energies are 82 eV for the symmetric state, and 83.2 eV for the antisymmetric state, so the antisymmetric state has the lower potential energy, like in the hydrogen molecular ion case, and unlike what you read in some books. The symmetric state has the lower energy because of lower kinetic energy, not potential energy.
Due to electron cloud merging, for the symmetric state the electron to electron repulsion energy is 3 eV lower than you would get if the electrons were point charges located at the nuclei. For the antisymmetric state, it is 5.8 eV lower.
As a consequence, the antisymmetric state also has less potential energy with respect to these repulsions. Adding it all together, the symmetric state has quite a lot less kinetic energy than the antisymmetric one.