| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.22 Unique ground state wave function
This derivation completes {A.8}. In particular, it
proves that ground states are unique, given a real, noninfinite,
potential that only depends on position. The derivation also proves
that ground states cannot become zero. So they can be taken to be
positive.
The basic idea is first to assume tentatively that there would be two
independent ground state wave functions. These could then be taken to
be orthonormal as usual. That means that the inner product of the two
wave functions would be zero. However, it can be shown, see below,
that ground state wave functions cannot cross zero. That means that
both wave functions can be taken to be everywhere positive. (The one
exception is at impenetrable boundaries, where the wave function is
forced to be zero, rather than positive. But that exception does not
change the argument here.) Now if you check the definition of the
inner product, you see that the inner product of two positive wave
functions is positive, not zero. But the orthonormality says that it
is zero. So there is a contradiction. That means that the made
assumption, that there are two independent ground states, must be
wrong. So the ground state must be unique.
Figure D.1:
Right: the absolute
value of the wave function has a kink at a zero crossing. Middle:
the kink has been slightly blunted. Right: an alternate way of
blunting.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(404,10...
... \put(166.8,43.7){\makebox(0,0)[l]{$\varepsilon_2$}}
\end{picture}
\end{figure}](img6260.gif) |
To finish the proof then, it must still be shown that ground states
that cross zero are not possible. Tentatively suppose that you had a
ground state whose wave function did cross zero. Near a zero
crossing, the wave function  will then look something like the
left part of figure D.1. (For a multi-dimensional wave
function, you can take this figure to be some arbitrary one-dimensional
cross section through the zero crossing.) Note from the figure that
the absolute value
will then look something like the
left part of figure D.1. (For a multi-dimensional wave
function, you can take this figure to be some arbitrary one-dimensional
cross section through the zero crossing.) Note from the figure that
the absolute value 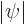 has a kink at the zero crossing.
has a kink at the zero crossing.
Next recall from {A.8} that 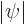 has the ground
state energy just like
has the ground
state energy just like  . So it should not be possible to
lower the energy below that of
. So it should not be possible to
lower the energy below that of 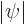 . But the problem is now
that the wave function shown in the middle in figure D.1
does have less energy. This wave function looks generally the
same as
. But the problem is now
that the wave function shown in the middle in figure D.1
does have less energy. This wave function looks generally the
same as 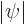 , except that the kink has been blunted just a
little bit. More precisely, this wave function has been prevented
from becoming any smaller than some very small number
, except that the kink has been blunted just a
little bit. More precisely, this wave function has been prevented
from becoming any smaller than some very small number
 .
.
To see why this wave function has less energy, compare what happens to
the kinetic and potential energies. The energy is the sum of a
kinetic energy integral 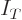 and a potential energy integral
and a potential energy integral 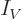 .
These are given by
.
These are given by
In the region that is blunted, the integrand of the kinetic energy
integral is now zero, instead of whatever positive value it had in the
left figure. The constant  has zero derivatives. So the
kinetic energy has been decreased noticeably.
has zero derivatives. So the
kinetic energy has been decreased noticeably.
You might at first think that the potential energy can compensate by
increasing more than the kinetic energy decreases. But that does not
work, because the integrand of the potential energy integral is
proportional to 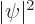 , and that is negligibly small in
the blunted region. In fact,
, and that is negligibly small in
the blunted region. In fact, 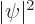 is no larger than
is no larger than
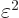 , and
, and  was a very small number. So,
if the kinetic energy decreases and the potential energy stays
virtually the same, the conclusion is unavoidable. The energy
decreases. The wave function in the middle in the figure has less
energy than the ones on the left. So the ones on the left cannot be
ground states. So ground state wave functions cannot cross zero.
was a very small number. So,
if the kinetic energy decreases and the potential energy stays
virtually the same, the conclusion is unavoidable. The energy
decreases. The wave function in the middle in the figure has less
energy than the ones on the left. So the ones on the left cannot be
ground states. So ground state wave functions cannot cross zero.
That is basically it. Unfortunately, there are a few loose ends in
the reasoning above. That is even if you ignore that
small
is not a valid mathematical concept. A number
is either zero or not zero; that is all in mathematics. The correct
mathematical statement is: “there is a number  small enough that the kinetic energy decrease exceeds the potential
energy increase.” (Note that
small enough that the kinetic energy decrease exceeds the potential
energy increase.” (Note that small enough
does
not imply small. All positive numbers less than 1 000 are small
enough to be less than 1 000.) But that is so picky.
More importantly, you might object that after blunting, the wave
function will no longer be normalized. But you can correct for that
by dividing the given expression of the expectation energy by the
square norm of the wave function. In particular, using a prime to
indicate a quantity after blunting the wave function, the correct
energy is
Now note that the square norm changes negligibly under the smoothing,
because its integrand involves 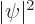 just like the potential
energy. So dividing by the square norm should not make a difference.
just like the potential
energy. So dividing by the square norm should not make a difference.
In fact, there is a trick to avoid the normalization problem
completely. Simply redefine the potential energy by a constant to
make the expectation energy zero. You can always do that; changing
the definition of the potential energy by constant does not make a
difference physically. And if the expectation energy 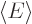 is
zero, then so is
is
zero, then so is 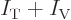 . Therefore the change in
energy due to blunting becomes
. Therefore the change in
energy due to blunting becomes
Comparing start and end, you see that the sign of the change in energy
is the same as the sign of the change in the kinetic and potential
energy integrals. Regardless of whether 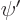 is normalized. And
the sign of the change in energy is all that counts. If it is
negative, you do not have a ground state. So if
is normalized. And
the sign of the change in energy is all that counts. If it is
negative, you do not have a ground state. So if 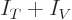 decreases
due to blunting, you do not have a ground state. Because of this
trick, the normalization problem can be ignored in the rest of the
derivations.
decreases
due to blunting, you do not have a ground state. Because of this
trick, the normalization problem can be ignored in the rest of the
derivations.
You might further object that the given arguments do not account for
the possibility that the wave function could cross zero with zero
slope. In that case, the integrand of the original kinetic energy
would be vanishingly small too. True.
But in one dimension, you can use the Cauchy-Schwartz inequality of
the notations section on 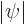 to show that the decrease in kinetic
energy will still be more than the increase in potential energy. For
simplicity, the coordinate
to show that the decrease in kinetic
energy will still be more than the increase in potential energy. For
simplicity, the coordinate  will be taken zero at the original zero
crossing, as in the middle graph of figure D.1. Now
consider the part of the blunted region at negative
will be taken zero at the original zero
crossing, as in the middle graph of figure D.1. Now
consider the part of the blunted region at negative  . Here
the original kinetic energy integral was:
. Here
the original kinetic energy integral was:
The first inequality above is the Cauchy-Schwartz inequality. The
final equality applies because the change in  is the integral of
its derivative. Comparing start and end above, the kinetic energy
decrease is at least
is the integral of
its derivative. Comparing start and end above, the kinetic energy
decrease is at least
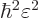

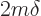 . On the other hand
for the increase in potential energy
. On the other hand
for the increase in potential energy
where 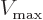 is the maximum (redefined) potential in the
region. (Note that if
is the maximum (redefined) potential in the
region. (Note that if  is not monotonuous,
is not monotonuous, 
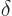 and
and
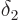 are defined as the points closest to the origin where
are defined as the points closest to the origin where
 is reached. So by definition
is reached. So by definition 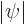 does not exceed
does not exceed
 .) It is seen that the maximum potential energy
decrease is proportional to
.) It is seen that the maximum potential energy
decrease is proportional to 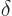 . However, the minimum
kinetic energy decrease is proportional to 1/
. However, the minimum
kinetic energy decrease is proportional to 1/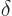 . So for
small enough
. So for
small enough 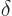 , potential energy increase cannot compete
with kinetic energy decrease. More specifically, taking
, potential energy increase cannot compete
with kinetic energy decrease. More specifically, taking 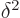 small compared to
small compared to 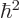

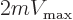 makes the
potential energy increase small compared to the kinetic energy
decrease. So the net energy will decrease, showing that the original
wave function is indeed not a ground state. (If
makes the
potential energy increase small compared to the kinetic energy
decrease. So the net energy will decrease, showing that the original
wave function is indeed not a ground state. (If 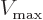 is
negative, the potential energy will decrease, and net energy decrease
is automatic.)
is
negative, the potential energy will decrease, and net energy decrease
is automatic.)
The same arguments normally apply for the blunted region at positive
 . However, there is a possible exception. If after
. However, there is a possible exception. If after  reaches zero, it stays zero, there will be no position
reaches zero, it stays zero, there will be no position
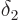 . At least not one vanishingly close to zero. To
deal with this possibility, a slightly more sophisticated blunting
can be used. That one is shown to the right in figure
D.1. Here the blunting region is taken to be symmetric
around the origin. The value of
. At least not one vanishingly close to zero. To
deal with this possibility, a slightly more sophisticated blunting
can be used. That one is shown to the right in figure
D.1. Here the blunting region is taken to be symmetric
around the origin. The value of 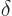 is taken as the smallest
distance from the origin where
is taken as the smallest
distance from the origin where  is reached. Therefore
once again
is reached. Therefore
once again 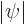 does not exceed
does not exceed  . Note that
the modified wave function now has some kinetic energy left. In
particular it has left
. Note that
the modified wave function now has some kinetic energy left. In
particular it has left
However, as seen above, the negative blunted part has kinetic energy
of at least 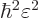

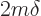 . So the
kinetic energy decrease is still at least half of what it was. That
is enough not to change the basic story.
. So the
kinetic energy decrease is still at least half of what it was. That
is enough not to change the basic story.
Note that in neither approach, the zero crossing point can be at an
impenetrable boundary. Neither blunted wave function is zero at 
 0 at it should be at an impenetrable boundary. That explains
why ground state wave functions can indeed become zero at impenetrable
boundaries. The ground state of the particle in a pipe provides an
example, chapter 3.5.
0 at it should be at an impenetrable boundary. That explains
why ground state wave functions can indeed become zero at impenetrable
boundaries. The ground state of the particle in a pipe provides an
example, chapter 3.5.
Also note the need to assume that the potential does not become
positive infinity. If the potential is positive infinity in a finite
region, then the wave function is in fact zero inside that
region. The particle cannot penetrate into such a region. Its
surface acts just like an impenetrable boundary.
How about wave functions in more than one dimension? That is easy, if
you will allow a very minor assumption. The minor assumption is that
there is at least a single crossing point where the gradient of  is continuous and nonzero. It does not have to be true at all the
zero crossing points, just at one of them. And in fact it does not
even have to be true for either one of the two supposed ground states.
It is enough if it is true for a single point in some linear
combination of them. So it is very hard to imagine ground states for
which the assumption would not apply.
is continuous and nonzero. It does not have to be true at all the
zero crossing points, just at one of them. And in fact it does not
even have to be true for either one of the two supposed ground states.
It is enough if it is true for a single point in some linear
combination of them. So it is very hard to imagine ground states for
which the assumption would not apply.
Accepting that assumption, things are straightforward. Take the
blunted wave function essentially like the middle graph in figure
D.1. The  -direction is now the direction of the
gradient at the point. However, rather than limiting the wave
function to stay above
-direction is now the direction of the
gradient at the point. However, rather than limiting the wave
function to stay above  , demand that it stays above
, demand that it stays above
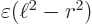

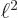 . Here
. Here  is the distance
from the considered zero crossing point, and
is the distance
from the considered zero crossing point, and 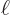 is a number small
enough that the variation in the gradient is no more than say 50%
within a distance
is a number small
enough that the variation in the gradient is no more than say 50%
within a distance 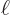 from the zero crossing point. There is then
again some kinetic energy left, but it is negligibly small. The
estimates in each cross section of the blunted region are essentially
the same as in the one-dimensional case.
from the zero crossing point. There is then
again some kinetic energy left, but it is negligibly small. The
estimates in each cross section of the blunted region are essentially
the same as in the one-dimensional case.
However, all that does require that one minor assumption. You might
wonder about pathological cases. For example, what if one wave
function is only nonzero where the other is zero and vice-versa? With
zero gradient at every single point of the zero crossings to boot? Of
course, you and I know that ground states are not just stupidly going
to be zero in sizable parts of the region. Why would the electron
stay out of some region completely? Would not its uncertainty in
position at least produce a very tiny probability for the elecron to
be inside them? But proving it rigorously is another matter. Then
there are somewhat more reasonable conjectures, like that a wave
function would become zero at a single point not at the boundary.
(That would still give a unique ground state. But would you not want
to know whether it really could happen?) How about fractal wave
functions? Or just discontinuous ones? In one dimension the wave
function must be continuous, period. A discontinuity would produce a
delta function in the derivative, which would produce infinite kinetic
energy. But in multiple dimensions, things become much less obvious.
(Note however that in real life, a noticeably singularity in  at
a point would require quite a singular potential at that point.)
at
a point would require quite a singular potential at that point.)
You might guess that you could use the approach of the right graph in
figure D.1 in multiple dimensions, taking the  coordinate in the direction normal to the zero crossing surface. But
first of all that requires that the zero crossing surface is
rectifiable. That excludes lone zero crossing points, or fractal
crossing surfaces. And in addition there is a major problem with
trying to show that the derivatives in directions other than
coordinate in the direction normal to the zero crossing surface. But
first of all that requires that the zero crossing surface is
rectifiable. That excludes lone zero crossing points, or fractal
crossing surfaces. And in addition there is a major problem with
trying to show that the derivatives in directions other than  remain small.
remain small.
There is however a method somewhat similar to the one of the right
graph that continues to work in more than one dimensions. In
particular, in three dimensions this method uses a small sphere of
radius 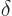 around the supposed point of zero wave function. The
method can show in, any number of dimensions, that
around the supposed point of zero wave function. The
method can show in, any number of dimensions, that 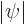 cannot
become zero. (Except at impenetrable boundaries as always.) The
method does not make any unjustified a priory assumptions like a
nonzero gradient. However, be warned: it is going to be messy. Only
mathematically inclined students should read the rest of this
derivation.
cannot
become zero. (Except at impenetrable boundaries as always.) The
method does not make any unjustified a priory assumptions like a
nonzero gradient. However, be warned: it is going to be messy. Only
mathematically inclined students should read the rest of this
derivation.
The discussion will use three dimensions as an example. That
corresponds, for example, to the electron of the hydrogen molecular
ion. But the same arguments can be made in any number of dimensions.
For example, you might have a particle confined in a two-dimensional
quantum well. In that case, the sphere around the point of zero wave
function becomes a circle. Similarly, in a one-dimensional quantum wire,
the sphere becomes the line segment 
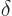
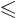

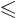
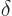 . If you have two nonconfined electrons instead of just
one, you are in six dimensions. All these cases can be covered
mathematically by generalizing the three-dimensional sphere to a
. If you have two nonconfined electrons instead of just
one, you are in six dimensions. All these cases can be covered
mathematically by generalizing the three-dimensional sphere to a
hypersphere.
A two-dimensional hypersphere is physically a
circle, and a one-dimensional hypersphere is a line segment. As discussed
in the notations section, a general  -dimensional hypersphere has
an
-dimensional hypersphere has
an  -dimensional
-dimensional volume
and surface
area
given by:
For example, 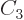

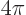 /3, so the above expressions give the
correct volume and surface of a sphere in three dimensions. In two
dimensions, the
/3, so the above expressions give the
correct volume and surface of a sphere in three dimensions. In two
dimensions, the volume
is physically the area of the
circle, and the area
is its perimeter. The
derivations will need that the  -dimensional infinitesimal
integration element is
-dimensional infinitesimal
integration element is
Here 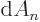 is an infinitesimal segment of the spherical surface
of radius
is an infinitesimal segment of the spherical surface
of radius  . You can relate this to the way that you do integration
in polar or spherical coordinates. However, the above expression does
not depend on exactly how the angular coordinates on hypersphere areas
are defined.
. You can relate this to the way that you do integration
in polar or spherical coordinates. However, the above expression does
not depend on exactly how the angular coordinates on hypersphere areas
are defined.
To show that points of zero wave function are not possible, once again
first the opposite will be assumed. So it will be assumed that there
is some point where 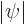 becomes zero. Then a contradiction will
be established. That means that the assumption must be incorrect;
there are no points of zero wave function.
becomes zero. Then a contradiction will
be established. That means that the assumption must be incorrect;
there are no points of zero wave function.
To find the contradiction, define a radial coordinate  as the
distance away from the supposed point of zero
as the
distance away from the supposed point of zero 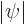 . Next at
every distance
. Next at
every distance  , define
, define 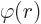 as the average value
as the average value
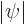 on the spherical surface of radius
on the spherical surface of radius  :
:
Function 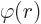 will need to be continuous for
will need to be continuous for 
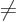 0,
otherwise the implied jump in wave function values would produce
infinite kinetic energy. For
0,
otherwise the implied jump in wave function values would produce
infinite kinetic energy. For 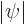 to become zero at
to become zero at 
 0,
as assumed, requires that
0,
as assumed, requires that 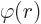 is also continuous at
is also continuous at 
 0 and that
0 and that 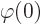
 0. (Note that
0. (Note that 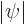 must be
continuous and zero at
must be
continuous and zero at 
 0. Otherwise it would have values
that stay a finite amount above zero however close you get to
0. Otherwise it would have values
that stay a finite amount above zero however close you get to 
 0. Then
0. Then 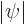 would not be zero in a meaningful sense. And
here we want to exclude points of zero wave function. Excluding
points of indeterminate wave function will be left as an exercise for
the reader. But as already mentioned, that sort of singular behavior
would require quite a singular potential.)
would not be zero in a meaningful sense. And
here we want to exclude points of zero wave function. Excluding
points of indeterminate wave function will be left as an exercise for
the reader. But as already mentioned, that sort of singular behavior
would require quite a singular potential.)
Take now some small sphere, of some small radius 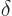 , around the
supposed point of zero wave function. The value of
, around the
supposed point of zero wave function. The value of  on the
outer surface of this sphere will be called
on the
outer surface of this sphere will be called  . It will be
assumed that there are no values of
. It will be
assumed that there are no values of 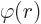 greater than
greater than 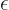 inside the sphere. (If there are, you can always reduce the value of
inside the sphere. (If there are, you can always reduce the value of
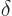 to get rid of them.)
to get rid of them.)
The blunting inside this sphere will now be achieved by replacing the
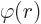 part of
part of 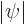 by
by  . So the blunted
wave function is:
. So the blunted
wave function is:
Consider now first what the corresponding increase in the potential
energy integral inside the sphere is:
Multiplying out the square, that becomes:
Since 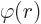 is nonnegative, it follows that the increase
in potential energy is limited as
is nonnegative, it follows that the increase
in potential energy is limited as
Note that the hypersphere formula for the volume of the sphere has
been used. The purpose is to make the final result valid in any
number  of dimensions, not just three dimensions. The remaining
integral in the above expression can be rewritten as
of dimensions, not just three dimensions. The remaining
integral in the above expression can be rewritten as
So finally
The next question is what happens to the kinetic energy. In
three-dimensional spherical coordinates, the kinetic energy after blunting
is
The initial kinetic energy is given by a similar expression, with
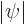 replacing
replacing 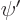 . Now the expression for the angular
derivatives in the integrand will be different in a different number
of dimensions. For example, in two-dimensional polar coordinates, there
will be no
. Now the expression for the angular
derivatives in the integrand will be different in a different number
of dimensions. For example, in two-dimensional polar coordinates, there
will be no  -derivative. But these angular derivatives are
unchanged by the blunting and drop out in the difference in kinetic
energy. So the decrease in kinetic energy becomes, after substituting
for
-derivative. But these angular derivatives are
unchanged by the blunting and drop out in the difference in kinetic
energy. So the decrease in kinetic energy becomes, after substituting
for 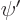 and simplifying:
and simplifying:
Since  does not depend on the angular coordinates, that can
be written
does not depend on the angular coordinates, that can
be written
The expression between square brackets is just the
 -derivative of
-derivative of  . So the decrease in kinetic energy
becomes, substituting in for
. So the decrease in kinetic energy
becomes, substituting in for 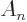 ,
,
Note that the kinetic energy does decrease. The right hand side is
positive. And if the maximum potential 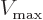 in the vicinity
of the point is negative, the potential energy decreases too. So that
cannot be a ground state. It follows that the ground state wave
function cannot become zero when
in the vicinity
of the point is negative, the potential energy decreases too. So that
cannot be a ground state. It follows that the ground state wave
function cannot become zero when 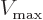 is negative or zero.
(Do recall that the potential
is negative or zero.
(Do recall that the potential 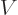 was redefined. In terms of the
original potential, there cannot be a zero if the potential is less
than the expectation value of energy.)
was redefined. In terms of the
original potential, there cannot be a zero if the potential is less
than the expectation value of energy.)
But how about positive 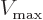 ? Here the factor
? Here the factor
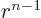 in the kinetic energy integral is a problem in more than one
dimension. In particular, if almost all the changes in
in the kinetic energy integral is a problem in more than one
dimension. In particular, if almost all the changes in  occur at small
occur at small  , the factor
, the factor 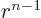 will make the kinetic
energy change small. Therefore there is no assurance that the kinetic
energy decrease exceeds the potential energy increase. So a ground
state cannot immediately be dismissed like in one dimension.
will make the kinetic
energy change small. Therefore there is no assurance that the kinetic
energy decrease exceeds the potential energy increase. So a ground
state cannot immediately be dismissed like in one dimension.
The solution is a trick. You might say that only a mathematician
would think up a trick like that. However, the author insists that he
is an aerospace engineer, not a mathematician. The first thing to
note that there is a constraint on how much  can change in
the outer half of the sphere, for
can change in
the outer half of the sphere, for 
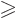
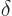 /2. There
the factor
/2. There
the factor 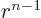 is at least
is at least 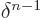
 2
2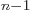 . So
the kinetic energy decrease is at least
. So
the kinetic energy decrease is at least
Now the remaining integral can be estimated by the Cauchy-Schwartz
inequality as before. Comparing this with the maximum possible
increase in potential energy will give a limit on the maximum change in
 in the outer half of the sphere. In particular
in the outer half of the sphere. In particular
where 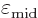 denotes the value of
denotes the value of  at the
midpoint
at the
midpoint 

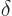
 2.
2.
If the above inequality is not satisfied, the kinetic energy decrease
would exceed the potential energy increase and it cannot be a ground
state. Note that if the sphere is chosen small, the relative decrease
in  is small too. For example, suppose you choose a sphere,
call it sphere 1, with a radius
is small too. For example, suppose you choose a sphere,
call it sphere 1, with a radius
In that case,
That means that  can at most decrease by 25% going from the
outside surface to the midpoint:
can at most decrease by 25% going from the
outside surface to the midpoint:
You might say, Why not?
And indeed, there would be
nothing wrong with the idea that almost all the change would occur in
the inner half of the sphere. But the idea is now to drive the
mathematics into a corner from which eventually there is no escape.
Suppose that you now define the inner half of sphere 1 to be a sphere
2. So the radius 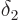 of this sphere is half that of sphere 1,
and its value of
of this sphere is half that of sphere 1,
and its value of  is
is
(If there are  values in the second sphere that exceed
values in the second sphere that exceed
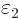 , you need to further reduce
, you need to further reduce 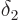 to get
rid of them. But all that does is reduce the possible changes in
to get
rid of them. But all that does is reduce the possible changes in
 even more.) In this second sphere, the allowed relative
decrease in its outer half is a factor 2 smaller than in sphere 1,
because
even more.) In this second sphere, the allowed relative
decrease in its outer half is a factor 2 smaller than in sphere 1,
because 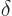 is a factor two smaller:
is a factor two smaller:
Now take the midpoint as the radius of a sphere 3. Then
Keep doing this and for sphere number  you get
you get
This must become zero for infinite  , because the sphere radii
contract to zero and
, because the sphere radii
contract to zero and  is zero at
is zero at 
 0. But it does
not! The allowed changes are simply too small to reach zero. Just
take the logarithm:
0. But it does
not! The allowed changes are simply too small to reach zero. Just
take the logarithm:
If 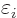 becomes zero, its logarithm must become minus
infinity. But the infinite sum does not become infinite. Just
use the Taylor series approximation
becomes zero, its logarithm must become minus
infinity. But the infinite sum does not become infinite. Just
use the Taylor series approximation 
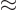

 :
:
The sum within square brackets is a geometric series that has a finite
limit, not an infinite one.
So there is a contradiction. At some stage the decrease in kinetic
energy must exceed the increase in potential energy. At that
stage, the energy can be reduced by applying the blunting. So the
assumed wave function cannot be a ground state.
You might still object that a Taylor series approximation is not
exact. But in the region of interest
and the additional ratio is just a constant, about 1.15, that does not
make a difference.
Woof.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(404,10...
... \put(166.8,43.7){\makebox(0,0)[l]{$\varepsilon_2$}}
\end{picture}
\end{figure}](img6260.gif)
![]()
![]()
![]()
![]() .
.![]() .
.![]() ,
,![]() .
.![]()
![]() .
.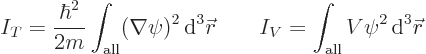
![]() ,
,![]()
![]() ,
,![]()
![]()
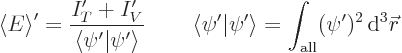
![]()
![]() .
.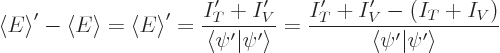
![]()
![]()
![]() .
.
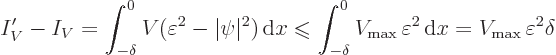
![]() .
.![]()
![]() .
.![]()
![]()
![]()
![]() .
.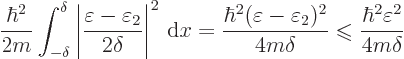
![]()
![]()
![]()
![]() -
-![]() ,
,![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]() -
-![]() -
-![]()
![]()
![]() .
.![]() ,
,![]()
![]()
![]() :
: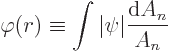
![]() ,
,![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]() .
.![\begin{displaymath}
I_V' - I_V =
\int\left[ V(\vert\psi\vert-\varphi(r)+\varepsilon)^2 - V (\vert\psi\vert)^2\right] { \rm d}^3{\skew0\vec r}
\end{displaymath}](img6287.gif)
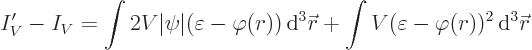
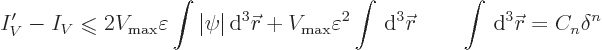
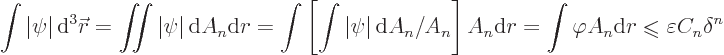
![\begin{displaymath}
I_T' = \frac{\hbar^2}{2m} \int
\Bigg[
\bigg(\frac{\partia...
...si'}}{\partial\phi}\bigg)^2
\Bigg]
{ \rm d}^3{\skew0\vec r}
\end{displaymath}](img6292.gif)
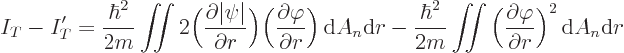
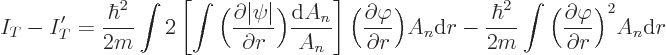
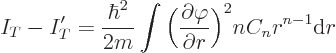
![]()
![]()
![]()
![]() ?
?![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() /
/![]()
![]()
![]()
![]() .
.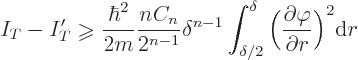
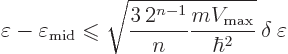
![]()
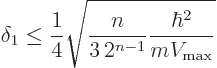
![]()
![]()