| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.26 Density of states
This note derives the density of states for particles in a box.
Consider the wave number space, as shown to the left in figure
6.1. Each point represents one spatial state. The first
question is how many points have a wave number vector whose length
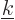 is less than some given value
is less than some given value  . Since the length of
the wave number vector is the distance from the origin in wave number
state, the points with
. Since the length of
the wave number vector is the distance from the origin in wave number
state, the points with 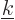
 form an octant of a sphere with
radius
form an octant of a sphere with
radius  . In fact, you can think of this problem as finding
the number of red points in figure 6.11.
. In fact, you can think of this problem as finding
the number of red points in figure 6.11.
Now the octant of the sphere has a volume
(in wave
number space, not a physical volume)
Conversely, every wave number point is the top-left front corner of
a little block of volume
where 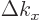 ,
, 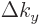 , and
, and 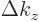 are
the spacings between the points in the
are
the spacings between the points in the  ,
,  , and
, and  directions respectively. To find the approximate number of points
inside the octant of the sphere, take the ratio of the two
directions respectively. To find the approximate number of points
inside the octant of the sphere, take the ratio of the two
volumes:
Now the spacings between the points are given in terms of the sides
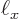 ,
, 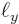 , and
, and 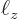 of the box containing the
particles as, (6.3),
of the box containing the
particles as, (6.3),
Plug this into the expression for the number of points in the octant
to get:
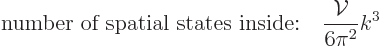 |
(D.12) |
where 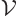 is the (physical) volume of the box
is the (physical) volume of the box
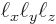 . Each wave number point corresponds to one
spatial state, but if the spin of the particles is
. Each wave number point corresponds to one
spatial state, but if the spin of the particles is 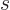 then each
spatial state still has
then each
spatial state still has 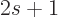 different spin values. Therefore
multiply by
different spin values. Therefore
multiply by 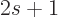 to get the number of states.
to get the number of states.
To get the density of states on a wave number basis, take the
derivative with respect to  . The number of states
. The number of states 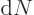 in a small wave number range
in a small wave number range 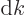 is then:
is then:
The factor 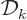 is the density of states on a wave number basis.
is the density of states on a wave number basis.
To get the density of states on an energy basis, simply eliminate  in terms of the single-particle energy
in terms of the single-particle energy 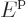 using
using 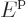

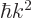

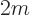 . That gives:
. That gives:
The used expression for the kinetic energy 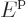 is only valid for
nonrelativistic speeds.
is only valid for
nonrelativistic speeds.
The above arguments fail in the presence of confinement. Recall that
each state is the top-left front corner of a little block in wave
number space of volume 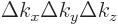 . The
number of states with wave number
. The
number of states with wave number 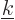 less than some given value
less than some given value  was found by computing how many such little block volumes are
contained within the octant of the sphere of radius
was found by computing how many such little block volumes are
contained within the octant of the sphere of radius  .
.
The problem is that a wave number 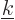 is only inside the sphere
octant if all of its little block is inside. Even if 99% of its
block is inside, the state itself will still be outside, not 99% in.
That makes no difference if the states are densely spaced in wave
number space, like in figure 6.11. In that case almost all
little blocks are fully inside the sphere. Only a thin layer of
blocks near the surface of the sphere are partially outside it.
is only inside the sphere
octant if all of its little block is inside. Even if 99% of its
block is inside, the state itself will still be outside, not 99% in.
That makes no difference if the states are densely spaced in wave
number space, like in figure 6.11. In that case almost all
little blocks are fully inside the sphere. Only a thin layer of
blocks near the surface of the sphere are partially outside it.
However, confinement in a given direction makes the corresponding
spacing in wave number space large. And that changes things.
In particular, if the  -dimension
-dimension 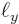 of the box containing the
particles is small, then
of the box containing the
particles is small, then 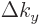

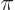

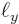 is large.
That is illustrated in figure 6.12. In this case, there are
no states inside the sphere at all if
is large.
That is illustrated in figure 6.12. In this case, there are
no states inside the sphere at all if  is less than
is less than
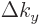 . Regardless of what (D.12) claims. In
the range
. Regardless of what (D.12) claims. In
the range 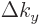
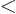

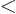
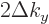 ,
illustrated by the red sphere in figure 6.12, the red sphere
gobbles up a number of states from the plate
,
illustrated by the red sphere in figure 6.12, the red sphere
gobbles up a number of states from the plate 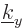

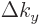 . This number of states can be estimated as
. This number of states can be estimated as
since the top of this ratio is the area of the quarter circle of
states and the bottom is the rectangular area occupied per state.
This expression can be cleaned up by noting that
with 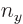
 1 for the lowest plate. Substituting for
1 for the lowest plate. Substituting for
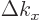 ,
, 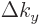 , and
, and 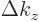 in terms
of the box dimensions then gives
in terms
of the box dimensions then gives
![\begin{displaymath}
\mbox{spatial states per plate:} \quad \frac{A}{4\pi}
\big...
...right)^2\bigg]
\qquad \mbox{if}\quad \bigg[\ldots\bigg] > 0 %
\end{displaymath}](img6356.gif) |
(D.13) |
Here 

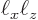 is the area of the quantum well and
is the area of the quantum well and
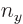
 1 is the plate number. For nonrelativistic speeds
1 is the plate number. For nonrelativistic speeds 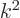 is proportional to the energy
is proportional to the energy 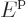 . Therefore the density of
states, which is the derivative of the number of states with respect
to energy, is constant.
. Therefore the density of
states, which is the derivative of the number of states with respect
to energy, is constant.
In the range 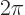

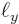
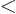

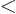
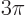

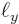 a second
quarter circle of states gets added. To get the number of additional
states in that circle, use
a second
quarter circle of states gets added. To get the number of additional
states in that circle, use 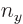
 2 for the plate number in
(D.13). For still larger values of
2 for the plate number in
(D.13). For still larger values of  , just keep
summing plates as long as the expression between the square brackets
in (D.13) remains positive.
, just keep
summing plates as long as the expression between the square brackets
in (D.13) remains positive.
If the  -dimension of the box is also small, like in a quantum
wire, the states in wave number space separate into individual lines,
figure 6.13. There are now no states until the sphere of
radius
-dimension of the box is also small, like in a quantum
wire, the states in wave number space separate into individual lines,
figure 6.13. There are now no states until the sphere of
radius  hits the line that is closest to the origin, having quantum
numbers
hits the line that is closest to the origin, having quantum
numbers 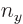

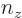
 1. Beyond that value of
1. Beyond that value of  ,
the number of states on the line that is within the sphere is
,
the number of states on the line that is within the sphere is
since the top is the length of the line inside the sphere and the
bottom the spacing of the states on the line. Cleaning up, that gives
![\begin{displaymath}
\mbox{spatial states per line:} \quad
\frac{\ell}{\pi} \bi...
...2 \bigg]^{1/2}
\qquad \mbox{if}\quad \bigg[\ldots\bigg] > 0 %
\end{displaymath}](img6359.gif) |
(D.14) |
with 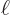

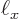 the length of the quantum wire. For still larger
values of
the length of the quantum wire. For still larger
values of  sum over all values of
sum over all values of 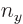 and
and 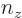 for which the
argument of the square root remains positive.
for which the
argument of the square root remains positive.
For nonrelativistic speeds, 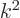 is proportional to the energy.
Therefore the above number of states is proportional to the square
root of the amount of energy above the one at which the line of states
is first hit. Differentiating to get the density of states, the
square root becomes an reciprocal square root.
is proportional to the energy.
Therefore the above number of states is proportional to the square
root of the amount of energy above the one at which the line of states
is first hit. Differentiating to get the density of states, the
square root becomes an reciprocal square root.
If the box is small in all three directions, figure 6.14,
the number of states simply becomes the number of points inside the
sphere:
![\begin{displaymath}
\mbox{spatial states per point:} \quad 1
\qquad \bigg[k^2 ...
...\right)^2
- \left(n_z\frac{\pi}{\ell_z}\right)^2 \bigg] > 0 %
\end{displaymath}](img6360.gif) |
(D.15) |
In other words, to get the total number of states inside, simply add a
1 for each set of natural numbers 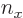 ,
, 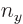 , and
, and 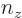 for which the expression in brackets is positive. The derivative with
respect to energy, the density of states, becomes a series of delta
functions at the energies at which the states are hit.
for which the expression in brackets is positive. The derivative with
respect to energy, the density of states, becomes a series of delta
functions at the energies at which the states are hit.
![]()
![]() .
.![]()
![]()
![]()
![]() .
.
![]() ,
,![]() ,
,![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.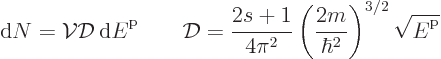
![]() .
.![]()
![]()
![]() .
.![]()
![]() -
-![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() .
.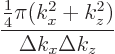
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() -
-![]()
![]()
![]()
![]()
![]()
![]() ,
,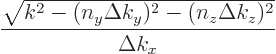
![]()