| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.27 Radiation from a hole
To find how much blackbody radiation is emitted from a small hole in a
box, first imagine that all photons move in the direction normal to
the hole with the speed of light 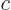 . In that case, in a time
interval
. In that case, in a time
interval 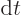 , a cylinder of photons of volume
, a cylinder of photons of volume 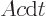 would leave through the hole, where
would leave through the hole, where  is the hole area. To get the
electromagnetic energy in that cylinder, simply multiply by
Planck’s blackbody spectrum
is the hole area. To get the
electromagnetic energy in that cylinder, simply multiply by
Planck’s blackbody spectrum 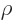 . That gives the surface
radiation formula except for an additional factor
. That gives the surface
radiation formula except for an additional factor 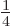 .
Half of that factor is due to the fact that on average only half of
the photons will have a velocity component in the direction normal to
the hole that is towards the hole. The other half will have a
velocity component in that direction that is away from the hole. In
addition, because the photons move in all directions, the average
velocity component of the photons that move towards the hole is only
half the speed of light.
.
Half of that factor is due to the fact that on average only half of
the photons will have a velocity component in the direction normal to
the hole that is towards the hole. The other half will have a
velocity component in that direction that is away from the hole. In
addition, because the photons move in all directions, the average
velocity component of the photons that move towards the hole is only
half the speed of light.
More rigorously, assume that the hole is large compared to
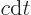 . The fraction of photons with velocity directions
within in a spherical element
. The fraction of photons with velocity directions
within in a spherical element 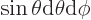 will be
will be
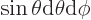

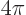 . The amount of these
photons that exits will be those in a skewed cylinder of volume
. The amount of these
photons that exits will be those in a skewed cylinder of volume
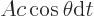 . To get the energy involved multiply by
. To get the energy involved multiply by
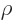 . So the energy leaving in this small range of velocity
directions is
. So the energy leaving in this small range of velocity
directions is
Integrate over all  and
and  up to 90 degrees to get
up to 90 degrees to get
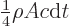 for the total energy that exits.
for the total energy that exits.
Note also from the above expression that the amount of energy leaving
per unit time, unit area, and unit solid angle is
where  is the angle from the normal to the hole.
is the angle from the normal to the hole.
![]() .
.![]() ,
,![]()
![]()
![]() .
.![]() .
.![]() .
.![]()
![]()
![]()
![]() .
.![]() .
.![]() .
.