8.2.2 Streamlines

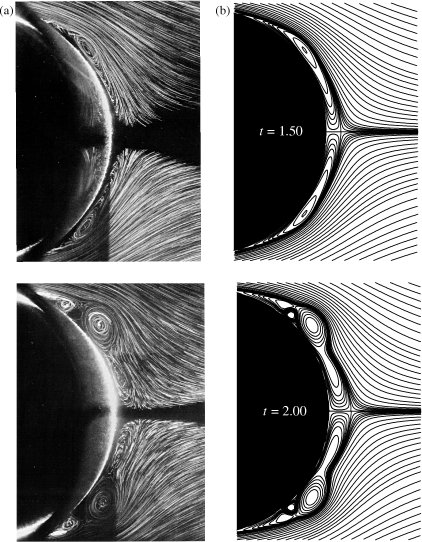
In this subsection we show that our computed streamlines do indeed predict the flow features observed in the experimental results very accurately.

**Figure 8.4:** Impulsively translated cylinder, : Instantaneous streamlines from vorticity redistribution ( $\Delta t=0.01; \epsilon _\Gamma =10^{-5}$ ); see subsection 8.2.2 for streamline values.
$\begin{figure}\par \epsffile{psi550.eps} \par\end{figure}$

**Figure 8.5:** Impulsively translated cylinder, : (a) Streamlines from experiment (Bouard & Coutanceau [29], used by permission); (b) Instantaneous streamlines from vorticity redistribution ( $\Delta t=0.01; \epsilon _\Gamma =10^{-5}$ ); see subsection 8.2.2 for streamline values.
$\begin{figure}\par \epsffile{psi550b.eps} \par \par \end{figure}$

**Figure 8.6:** Impulsively translated cylinder, : Instantaneous streamlines from vorticity redistribution ( $\Delta t=0.01; \epsilon _\Gamma =10^{-5}$ ); see subsection 8.2.2 for streamline values.
$\begin{figure}\par \epsffile{psi3000.eps} \par\end{figure}$

**Figure 8.7:** Impulsively translated cylinder,: (a) Streamlines from experiment (Bouard & Coutanceau [29], used by permission); (b) Instantaneous streamlines from vorticity redistribution ( $\Delta t=0.01; \epsilon _\Gamma =10^{-5}$ ); see subsection 8.2.2 for streamline values.
$\begin{figure}\par \epsffile{psi3000b.eps} \par\par \end{figure}$

**Figure 8.8:** Impulsively translated cylinder, : (a) Streamlines from experiment (Bouard & Coutanceau [29], used by permission); (b) Instantaneous streamlines from vorticity redistribution ( $\Delta t=0.01; \epsilon _\Gamma =10^{-6}$ ); see subsection 8.2.2 for streamline values.
$\begin{figure}\par \epsffile{psi9500b.eps} \par \par \end{figure}$

**Figure 8.8:** (continued.)
$\begin{figure}\par \epsffile{psi9500c.eps} \par\par \end{figure}$

Computed streamlines are shown in figures 8.4, 8.6 and 8.8 for

, 3,000, and 9,500 respectively. Note that the fluid comes from the left of the cylinder. The characteristic feature is the presence of a large recirculating flow region of closed streamlines behind the cylinder. The streamwise length of this recirculating region, also known as the wake length [29], grows in time. The wake length at any fixed time is smaller for increasing Reynolds number.

A comparison of our computed streamlines with those obtained in the experiment of Bouard & Coutanceau [29] is shown in figures 8.5, 8.7, and 8.8 for

, 3,000, and 9,500 respectively. Our streamlines in the large recirculating flow region behind the cylinder are in good visual agreement with those of the experiment. In addition to this large recirculating flow region, a number of smaller recirculating flow regions along the rear half of the cylinder surface seen in the experiment are also observed in our computations. As shown by Lecointe & Piquet [123], some of the earlier finite difference computations were not able to reproduce these smaller recirculating flow regions.

For completeness, we now give the parameters of our figures 8.4 through 8.8. Using the usual left-handed

coordinate system with origin at the center of the cylinder, the figure dimensions and streamline contour values are as follows: in figure 8.4 for

and figure 8.6 for

has the range [-1.5,3.0] and

has the range [-1.4,1.4]; in both these figures, the streamline contour values are 0, $\pm$ {0.001, 0.0025, 0.005, 0.01, 0.03, 0.05, 0.07, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.875, 0.95, 1.025, 1.10, 1.175, and 1.25 }. In figure 8.5 for

has the range [-0.54,3.75],

has the range [-1.63,1.63], and the streamline values are same as above. In figures 8.7 for

has the range [-0.16,3.10],

has the range [-1.26,1.26], and the streamline values are same as above. In figure 8.8 for

has the range [-0.25,1.75] and

has the range [-1.05,1.05]; the streamline values are 0, $\pm$ {0.001, 0.003, 0.005, 0.007, 0.01, 0.015, 0.027, 0.04, 0.06, 0.08, 0.1, 0.125, 0.15, 0.18, 0.21, 0.24, 0.27, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, and 0.7 }.

In view of the fact that an impulsive start cannot be exactly reproduced experimentally, the agreement between our computation and the experimental data for the streamlines is excellent. However, many other computations, [40,117,134] for example, have also shown such good visual agreement between their computed streamline patterns and those of the experiments. A much stronger test is a comparison of higher order derivatives of the streamfunction, such as the velocity and vorticity fields, and the drag force on the cylinder for example. In the next subsection we compare our computed velocity field with those obtained from both experiments as well as other computations.