7.2.2 Vorticity field

**Figure 7.3:** Vortex pair, : Vorticity along the connecting line at times $\tau =0.082$ & . The solid lines are exact and circles are vorticity redistribution solutions.
$\begin{figure}\centerline{\epsfxsize=15cm\epsfbox{dxvor0.eps} }\end{figure}$

**Figure 7.4:** Vortex pair, : Isovorticity contours (a) at time $\tau =0.082$ : $\omega = 5.00$ , 3.85, 2.70, 1.55, & 0.40; (b) at time $\tau =0.202$ : $\omega = 1.40$ , 1.10, 0.80, 0.50, & 0.20. The solid lines are exact and circles are vorticity redistribution solutions.
$\begin{figure}\centerline{\epsfxsize=12cm\epsfbox{diso10.eps} } \centerline{\epsfxsize=12cm\epsfbox{diso20.eps} }\end{figure}$

For the Stokes flow

, the exact solution exists: it is simply a superposition of two single diffusing vortices. Figure 7.3 shows the vorticity distribution along the line connecting the initial point vortices. There is excellent agreement between the exact solution and the computed vorticity. This is also evident from the computed vorticity lines figure 7.4. As demonstrated by Van Dommelen [235], a standard random walk approach would experience considerable difficulty with this flow since vanishing vorticity is there approximated by roughly equal amounts of negative and positive vortices of the initial strength.

Unfortunately, for nonzero Reynolds number no exact analytical solution is available to show how well the nontrivial convection effects are represented. Instead, we use the second order expansion derived by Van Dommelen & Shankar [230] which is valid for sufficiently small times. To obtain high resolution for small times, we performed the computations in this section at $\Delta \tau= 0.00025$ .

**Figure 7.5:** Vortex pair, : Isovorticity contours for a counter-rotating vortex pair. (a) at time $\tau =0.01025$ : $\omega = 40$ , 24, & 8; (b) at time $\tau =0.02050$ : $\omega = 20$ , 12, & 4. The dashed and solid lines represent orders of approximation in the analytical solution. Circles are vorticity redistribution solutions.
$\begin{figure}\centerline{\epsfxsize=12cm\epsfbox{siso150.eps} } \centerline{\epsfxsize=12cm\epsfbox{siso250.eps} } \vspace{-3mm}\end{figure}$

Figure 7.5 shows vorticity contours for Reynolds number

at two early times. The dashed curves in this graph represent the first order solution given by a simple superposition of single vortex solutions, while the solid curves include the next order in the small time expansion developed by Van Dommelen & Shankar [230]. The difference between the curves represents nontrivial convection effects. Since the two curves are close together in figure 7.5(a), we expect the small time approximations to be very accurate; hence the exact solution should be close to the solid curve. Our computations do reproduce this expected curve closely. We consider this to be excellent performance of both the small time expansion and our numerical scheme (especially for a vortex method with an arbitrary point distribution). Note that the time is no longer truly small: the vortices have already expanded to a size comparable to their distance!

At still later times, the small time expansion is probably no longer accurate, since it is based on the approximation that the size of the vortices is small compared to their distance. The inaccuracy is reflected in sizeable differences between the solid and dashed curves in figure 7.5(b). While the exact solution is now no longer certain, we still believe that it is accurately represented by our numerical solution. One reason is that the computed solution is closer to the solid curve; secondly, we expect the next higher-order term in the small time expansion to have three periods along a contour, which seems to agree with the number of curve crossings in figure 7.5. Table 7.2 shows the number of vortices and computational times at $\tau =0.202$ . The computations were carried out in 32 bit precision on a VAX4000-300 computer running VMS V6.0.

**Table 7.2:** Computational times for counter-rotating vortices at $\tau =0.202$ and $\Delta \tau =0.002$ .
Decay of a vortex pair
Reynolds	Number of	Convection	Diffusion
number	vortices	CPU secs	CPU secs
0	2981	0	2796
10	3525	2593	3524
50	5307	4303	5631

**Figure 7.6:** Vortex pair, : The effect of using exponentially decaying core shapes instead of algebraically decaying ones.
$\begin{figure}\centerline{\epsfxsize=12cm\epsfbox{siso1_c4.eps} } \centerline{\epsfxsize=12cm\epsfbox{siso2_c4.eps} }\end{figure}$

This study used algebraically decaying vortex cores, rather than the somewhat more usual exponentially decaying ones [17]. To check the effect, we repeated the computation of figure 7.5 using exponentially decaying cores: we used a second-order Gaussian core instead of (6.3) for convection, while at the end of the computation, the vorticity was evaluated using a fourth-order Gaussian core (6.13). The results in figure 7.6 show that the effect is negligible, although the Gaussian results seem slightly less accurate based on the comparison with the small time expansion at the earlier time.

**Figure 7.7:** Vortex pair: Isovorticity contours $\omega =$ 5, 3, & 1 at time $\tau =0.082$ for different Reynolds numbers.
$\begin{figure}\centerline{\epsfysize=18cm\epsfbox{iso1.eps} }\end{figure}$

**Figure 7.8:** Vortex pair: Isovorticity contours $\omega =$ 1.7, 1.5, ..., 0.1 at time $\tau =0.202$ for different Reynolds numbers.
$\begin{figure}\centerline{\epsfysize=18cm\epsfbox{iso2.eps} }\end{figure}$

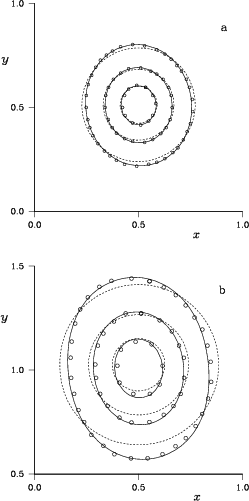
The small time expansion also predicts an increased symmetry of the vorticity distribution about the line connecting the vortex centers for increasing Reynolds numbers. That is evident in the vorticity contours of figure 7.7. At later times the results are considerably less symmetric, as shown in figure 7.8. In particular, the outer contour line at Reynolds number 50 seems to develop a leeward tail similar to the one found by Buntine and Pullin [32]. Their case of axisymmetric strain is equivalent to no strain after rescaling.

**Figure 7.9:** Vortex pair: Maximum vorticity for different Reynolds numbers. Stokes represents the exact solution for .
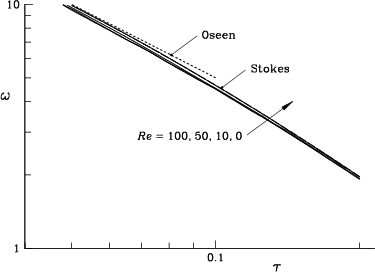$\begin{figure}{\hspace{-10mm} \centerline{\epsfxsize=15.5cm\epsfbox{max.eps} }}\end{figure}$

Our vorticity contour lines are close to those of Ohring and Lugt [166], although there seem to be some minor differences in the maximum value. Figure 7.9 depicts our results for the maximum vorticity as a function of time, along with the Oseen (small time or single vortex) and Stokes (large time) values. Our results follow the Stokes curve closely regardless of Reynolds number; this agrees with the results of Lo and Ting [132] for a similar flow.

**Figure 7.10:** Vortex pair: Distance of the point of maximum vorticity from the symmetry plane. Stokes represents the exact solution for .
$\begin{figure}{\hspace{-10mm} \centerline{\epsfxsize=15.5cm\epsfbox{xtot.eps} }}\end{figure}$

Figure 7.10 shows the distance of the vorticity maximum away from the symmetry line for Reynolds numbers 0, 10, 50, and 100. While a maximum is hard to locate in a vortex method with an arbitrary distribution of vortices, our results agree well with the exact Stokes solution (

) and with the results of Ohring and Lugt. In particular we agree with the conclusion of Ohring and Lugt that the maximum moves away from the symmetry plane at all times.

**Figure 7.11:** Vortex pair: Circulation in a half plane for different Reynolds numbers. Stokes represents the exact solution for .
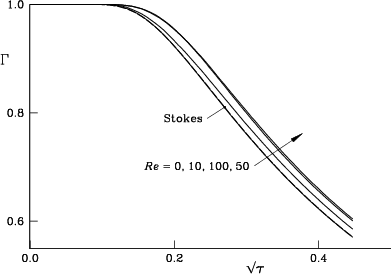$\begin{figure}{\hspace{-8mm} \centerline{\epsfxsize=15.5cm\epsfbox{circ.eps} }}\end{figure}$

Figure 7.11 shows the decay of the circulation in a half plane with time. We find no dramatic change in circulation with Reynolds number, although the circulation at higher Reynolds numbers decays somewhat more slowly. Our results at zero Reynolds number are almost identical to the exact Stokes solution. These results agree with those of Ohring and Lugt [166]. They also agree with the results of Buntine and Pullin [32] for a smoothed initial condition. Their results at Reynolds numbers 40 and 160 are indistinguishable, similar to our results at 50 and 100. Our curve for Reynolds number 100 ends up between those for 10 and 50.

For this flow, the velocity increases without bound when the Reynolds number increases, especially for small times. This leads to almost singular convection terms at high Reynolds numbers. Yet, our numerical results show that the redistribution method captures such strong convection effects very accurately. Further evidence of the accuracy and reliability of our method, including longer times, will be presented in the next section in which we discuss the propagation or drift velocity of the vortex pair.