7.2.3 Drift velocity

In the previous subsection we verified our numerical solution against a small time prediction for the vorticity field. In this section we will verify the numerical results for longer times against analytical predictions. In particular, we will examine the path and the velocity of the vortex pair. Those are important quantities in many practical applications. For example, a vortex pair provides a simple model for investigating the trailing vortices behind the wings of large aircrafts [131,167,223,253]; these vortices persist over long distances and are hazardous for smaller aircrafts in the vicinity of these vortices. Hence, it is important to know where the vortices end up. As an other example, the trailing vortices from a ship are also modeled by a vortex pair [141,194,226]; and the interactions of these vortices with the free surface of the sea produce characteristic signatures in radar images.

The drift velocity of two counter-rotating point vortices in an inviscid (to be precise, for $Re=\infty$ and $t=\tau\,Re$ finite) fluid is simple: the vortex pair drifts in the direction of the symmetry line (here the $y$-axis) at constant speed [230]. Further, in the inviscid case the positions of the vortices are simple to identify since the point vortices remain point vortices

However, in a viscous fluid the vortex pair diffuses, and changes shape and speed as it drifts. Hence, before we can compare the numerical results, we need to define first what point will be taken as the ``position" of the vortex pair. Different authors have used different points to measure the position; the time derivatives of these different points imply different drift velocities. We will first review some of these definitions. Since the flow is symmetric about the $y$-axis, we will focus on the flow in one half plane bounded by this symmetry line. One way to define a position of the vortex in the chosen half plane is to average over the vorticity:

$$y_c\;=\;\frac{\int \int\,y\,\omega\;dx\,dy}{\int \int\,\omega\;dx\,dy} \quad \ ,$$ (7.7)

where the integration is over the half plane. We will define the drift velocity obtained as the time derivative of $y_c$ to be the vortex center velocity $v_c$. Instead, Saffman [191] defines the vortex position to be

$$y_g\;=\;\frac{\int \int\,x\,y\,\omega\;dx\,dy}{\int\int\,x\,\omega\;dx\,dy} \quad \ .$$ (7.8)

We will denote the time derivative of $y_g$ to be the velocity $v_g$. Next, Ohring and Lugt [166] define the vortex position to be the location of the vorticity extremum, giving still a different velocity. In addition to these drift velocities, we can define an average velocity $\bar v$ in the direction of propagation as

$$\bar{v}\;=\;\frac{\int \int\,v\,\omega\;dx\,dy}{\int \int\,\omega\;dx\,dy} \quad \ ,$$ (7.9)

where $v$ is the component of the velocity field in the direction of propagation.

The limiting behaviors of the drift velocities defined above are investigated by Van Dommelen & Shankar [230] for small times, for small Reynolds numbers, and for large times using asymptotic expansions. In the following paragraphs, we compare the numerical results obtained using the vorticity redistribution method with the analytical solutions obtained there. The Reynolds number in the computation ranges from 0 to 100 based on the initial drift velocity. The computational results presented in this subsection were obtained at a diffusion time step $\Delta \tau =0.002$ and were repeated at $0.004$ to verify their accuracy. At the highest Reynolds number $Re=100$, we halved the time step again (to 0.001) to eliminate some unsightly, but inconsequential wiggles. In addition, for shorter times, computations were conducted at a still smaller time step ( $\Delta \tau= 0.00025$) to verify very small perturbations in the small time analytical solution.

Figure 7.12: Vortex pair: Average velocity $\bar v$, vortex center velocity $v_c$, and asymptotic velocity $v_g$ for vanishing Reynolds number. Short dash curves and dot dash curves represent the small time and the long time analytical solutions respectively.

Figure 7.12 shows analytical and semi-analytical results of Van Dommelen & Shankar [230] for the computed velocities $\bar v$, $v_c$ and $v_g$ for Reynolds number $Re=0$, as well as the small and large time expansions for that case. At small times, the average velocity $\bar v$ and the vortex center velocity $v_c$ remain exponentially close to the unit inviscid drift velocity. On the other hand, the velocity $v_g$ decreases proportional to the diffusion time $\tau$. Figure 7.12 also shows that the asymptotic values for the average velocity $\bar v$ and velocity $v_g$ for large times are still quite inaccurate at the maximum times presented here. The computed vortex center velocity $v_c$ tends to the computed velocity $v_g$ for large times; but the computed average velocity $\bar v$ remains larger than these two velocities by about $10\%$ [230].

Figure 7.13: Vortex pair: Deviation in average velocity $\bar v$ from the inviscid drift velocity. Short dash curves represent the small time analytical solutions. Stokes represents the exact solution for $Re=0$ and the asymptotic solution for large time for any Reynolds number.

Figure 7.14: Vortex pair: Deviation in vortex center velocity $v_c$ from the inviscid drift velocity. Short dash curves represent the small time analytical solutions. Stokes represents the exact solution for $Re=0$ and the asymptotic solution for large time for any Reynolds number.

As shown in figures 7.13 and 7.14, our computed results at a very fine time step ( $\Delta \tau= 0.00025$) correctly follow the analytical predictions for small times [230]. Note that this indicates excellent performance of the numerical method: the graph verifies very small deviations from the inviscid drift velocity. Furthermore, the velocity is almost singular at those times. In figures 7.13 and 7.14, the exact Stokes solution for $Re=0$, has also been shown. At larger times all computed curves should approach the Stokes curve since the decay of the circulations of the vortices reduces the effects of convection. This is consistent with our numerical results.

Figure 7.15: Vortex pair: Average velocity $\bar v$ for different Reynolds numbers. Short dash curves represent the small time analytical solutions. Stokes represents the exact solution for $Re=0$.

Figure 7.16: Vortex pair: Vortex center velocity $v_c$ for different Reynolds numbers. Short dash curves represent the small time analytical solutions. Stokes represents the exact solution for $Re=0$.

Figure 7.17: Vortex pair: Asymptotic velocity $v_g$ for different Reynolds numbers. Short dashed curves represent the small time analytical solutions. Stokes represents the exact solution for $Re=0$.

Figure 7.18: Vortex pair: Average velocity $\bar v$, vortex center velocity $v_c$ and asymptotic velocity $v_g$ for Reynolds number 100.

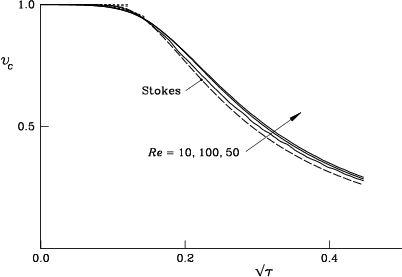
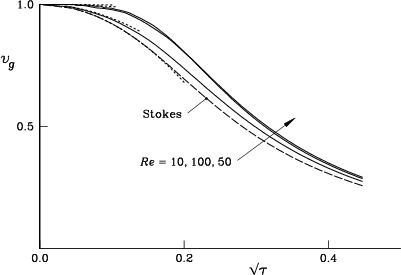
Figures 7.15, 7.16, and 7.17 show the computed average velocity $\bar v$, vortex center velocity $v_c$ and the velocity $v_g$ for Reynolds numbers 10, 50, and 100. No dramatic changes from Stokes flow are observed for the studied Reynolds numbers. Moreover, the different computed velocities have an interesting tendency to approach each other when the Reynolds number increases. For example, figure 7.18 compares these velocities at Reynolds number 100. Theoretical reasons why this would be so can be found in Van Dommelen & Shankar [230].