| A New Mesh-Free Vortex Method |
|
Shankar Subramaniam |
|
7.2.1 Governing equations
The flow studied here starts from two counter-rotating point vortices.
We use the same nondimensionalization as for a single point vortex
in subsection 7.1.1, but in addition we now chose the
characteristic length  as the distance between the initial
point vortices. This leads again to the vorticity diffusion equation
as the distance between the initial
point vortices. This leads again to the vorticity diffusion equation
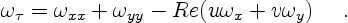 |
(7.4) |
However, the initial condition is now:
 |
(7.5) |
This vortex system will drift in the direction
normal to the line connecting the vortices.
Using our normalizations, the
initial drift velocity will be unity (which explains our choice of
normalizations). The Reynolds number
 can therefore also be considered
to be based on the
initial drift velocity and the vortex spacing.
can therefore also be considered
to be based on the
initial drift velocity and the vortex spacing.
The velocity again follows from the Biot-Savart law [14],
or equivalently from the streamfunction 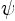 :
:
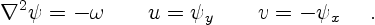 |
(7.6) |
![]() :
: