Next: The propagation velocity.
Up: The heat equation.
Previous: A note on
Parabolic equations such as the heat equation usually have smooth
solutions. Even if we prescribe an initial condition which is
singular, the heat equation will immediately smooth out this
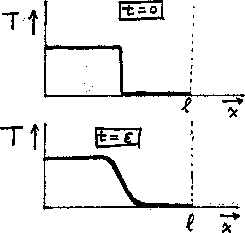
singularity. As an example, assume that we prescribe an initial
condition with a jump in temperature, in which the wall and the first
half of the bar are at 100 degrees and the second half at zero
degrees. This initial condition is shown as a temperature profile, or
T,x-plane, in figure 3. The jump is singular: at
it, the second and higher derivatives are infinite. But at a time
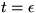 that is even slightly greater than zero, diffusion of
heat has caused the jump to diffuse out into a steep but smooth slope,
and all derivitives do now exist.
that is even slightly greater than zero, diffusion of
heat has caused the jump to diffuse out into a steep but smooth slope,
and all derivitives do now exist.
Figure 3:
Smoothing of a singularity.
 |
Next: The propagation velocity.
Up: The heat equation.
Previous: A note on
