Next: About evolution equations.
Up: The heat equation.
Previous: Smoothness of the
A property related to the smoothness of the solutions is that the heat
equation allows an infinite speed of propagation. At any time greater
than zero, the temperature at the right end will be greater than zero.
It will be extremely small at small times, but never exactly zero.
This implies that extremely small amounts of heat from the left half
of the bar reach the right end immediately, which is only possible if
it can propagate with infinite speed.
You could ignore extremely small amounts of heat and only
look at the typical thickness of the layer in the right half in
which most of the heat ends up. But even then, the thickness
of this layer is proportional to 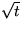 , and taking the
derivative, the velocity of expansion of the layer is initially
infinite. Physically, of course, the velocity of propagation must
be finite, so some of the physics has been lost in
deriving the heat equation.
, and taking the
derivative, the velocity of expansion of the layer is initially
infinite. Physically, of course, the velocity of propagation must
be finite, so some of the physics has been lost in
deriving the heat equation.
Next: About evolution equations.
Up: The heat equation.
Previous: Smoothness of the
![]() , and taking the
derivative, the velocity of expansion of the layer is initially
infinite. Physically, of course, the velocity of propagation must
be finite, so some of the physics has been lost in
deriving the heat equation.
, and taking the
derivative, the velocity of expansion of the layer is initially
infinite. Physically, of course, the velocity of propagation must
be finite, so some of the physics has been lost in
deriving the heat equation.