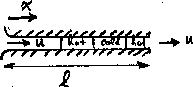The convection equation.

  A problem governed by quite a different PDE is shown in figure 5. It is convection of entropy through a pipe. A fluid enters the pipe at the left hand end, and flows out of the right hand side. It will be assumed that the flow is inviscid and nonconducting, in which case the entropy s of any fixed amount of fluid is constant. We will also assume that the flow is one-dimensional and that the flow velocity u in the pipe is constant. Since the entropy of the fluid is fixed, the entropy distribution moves along with the fluid towards the right. And since the pressure in the pipe will be constant, changes in entropy will be reflected by corresponding changes in temperature, so we will see hot and cold regions flow towards the right with speed u.

  

Figure 5: Convection in a pipe.