Characteristic lines.

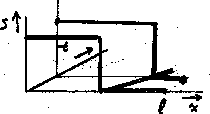
  When the initial condition has a singularity such as a jump, it will propagate with speed u, as any other part of the wave. In the x,t-plane, the singularity then propagates along a line with slope dx/dt equal to u. Lines with this slope are called characteristic lines of the PDE. The characteristic lines are shown in figure 7; the characteristic line along which the jump in our example propagates is shown thickened. Figure 8 shows a three-dimensional view of the propagation of the singularity along its characteristic line.

  

Figure 7: Characteristic lines.

  

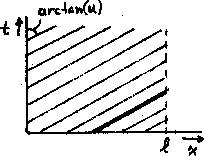Figure 8: Singularity propagation.