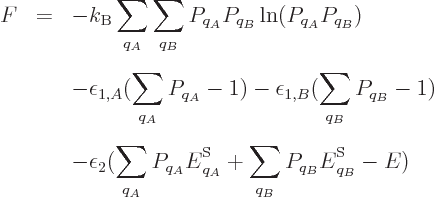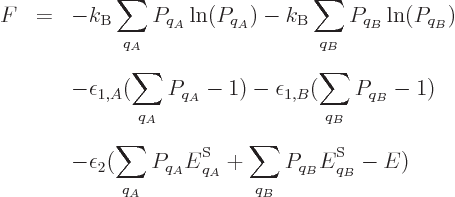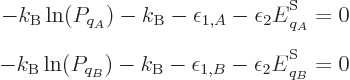| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.60 Checks on the expression for entropy
According to the microscopic definition, the differential of the entropy
 should be
should be
where the sum is over all system energy eigenfunctions 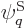 and
and 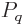 is their probability. The differential can be simplified to
is their probability. The differential can be simplified to
the latter equality since the sum of the probabilities is always one,
so 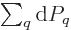
 0.
0.
This is to be compared with the macroscopic differential for the
entropy. Since the macroscopic expression requires thermal
equilibrium, 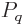 in the microscopic expression above can be equated
to the canonical value
in the microscopic expression above can be equated
to the canonical value 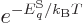

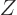 where
where 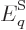 is the
energy of system eigenfunction
is the
energy of system eigenfunction 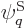 . It simplifies the
microscopic differential of the entropy to
. It simplifies the
microscopic differential of the entropy to
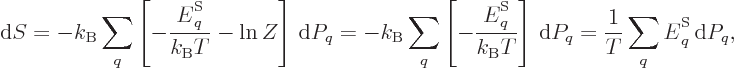 |
(D.38) |
the second inequality since 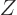 is a constant in the summation and
is a constant in the summation and
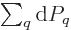
 0.
0.
The macroscopic expression for the differential of entropy is given by
(11.18),
Substituting in the differential first law (11.11),
and plugging into that the definitions of  and
and 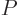 ,
,
and differentiating out the product in the first term, one part drops
out versus the second term and what is left is the differential for
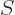 according to the microscopic definition (D.38). So, the
macroscopic and microscopic definitions agree to within a constant on
the entropy. That means that they agree completely, because the
macroscopic definition has no clue about the constant.
according to the microscopic definition (D.38). So, the
macroscopic and microscopic definitions agree to within a constant on
the entropy. That means that they agree completely, because the
macroscopic definition has no clue about the constant.
Now consider the case of a system with zero indeterminacy in energy.
According to the fundamental assumption, all the eigenfunctions with
the correct energy should have the same probability in thermal
equilibrium. From the entropy’s point of view, thermal
equilibrium should be the stable most messy state, having the maximum
entropy. For the two views to agree, the maximum of the microscopic
expression for the entropy should occur when all eigenfunctions of the
given energy have the same probability. Restricting attention to only
the energy eigenfunctions 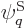 with the correct energy, the
maximum entropy occurs when the derivatives of
with the correct energy, the
maximum entropy occurs when the derivatives of
with respect to the 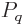 are zero. Note that the constraint that the
sum of the probabilities must be one has been added as a penalty term
with a Lagrangian multiplier, {D.48}. Taking
derivatives produces
are zero. Note that the constraint that the
sum of the probabilities must be one has been added as a penalty term
with a Lagrangian multiplier, {D.48}. Taking
derivatives produces
showing that, yes, all the 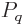 have the same value at the maximum
entropy. (Note that the minima in entropy, all
have the same value at the maximum
entropy. (Note that the minima in entropy, all 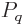 zero except one,
do not show up in the derivation;
zero except one,
do not show up in the derivation; 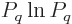 is zero when
is zero when 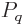
 0,
but its derivative does not exist there. In fact, the infinite
derivative can be used to verify that no maxima exist with any of the
0,
but its derivative does not exist there. In fact, the infinite
derivative can be used to verify that no maxima exist with any of the
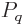 equal to zero if you are worried about that.)
equal to zero if you are worried about that.)
If the energy is uncertain, and only the expectation energy is known,
the penalized function becomes
and the derivatives become
which can be solved to show that
with 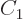 and
and 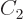 constants. The requirement to conform with the
given definition of temperature identifies
constants. The requirement to conform with the
given definition of temperature identifies 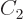 as
as 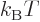 and the
fact that the probabilities must sum to one identifies
and the
fact that the probabilities must sum to one identifies 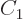 as
1/
as
1/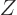 .
.
For two systems  and
and 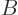 in thermal contact, the probabilities of
the combined system energy eigenfunctions are found as the products of
the probabilities of those of the individual systems. The maximum of
the combined entropy, constrained by the given total energy
in thermal contact, the probabilities of
the combined system energy eigenfunctions are found as the products of
the probabilities of those of the individual systems. The maximum of
the combined entropy, constrained by the given total energy  ,
is then found by differentiating
,
is then found by differentiating
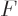 can be simplified by taking apart the logarithm and noting that
the probabilities
can be simplified by taking apart the logarithm and noting that
the probabilities 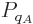 and
and 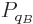 sum to one to give
sum to one to give
Differentiation now produces
which produces 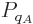

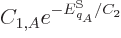 and
and
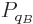

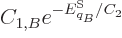 and the common constant
and the common constant  then
implies that the two systems have the same temperature.
then
implies that the two systems have the same temperature.
![]()
![\begin{displaymath}
{\rm d}S = -k_{\rm B}{\rm d}\left[\sum_q P_q \ln P_q\right]
\end{displaymath}](img7232.gif)
![\begin{displaymath}
{\rm d}S = - k_{\rm B}\sum_q \left[\ln P_q + 1\right]{ \rm d}P_q
= - k_{\rm B}\sum_q \ln P_q{ \rm d}P_q,
\end{displaymath}](img7233.gif)
![]()
![]()
![]()
![]()
![]()
![]() .
.![\begin{displaymath}
{\rm d}S = \frac{1}{T} { \rm d}\left[\sum_qP_q {\vphantom'...
...c{{\rm d}{\vphantom' E}^{\rm S}_q}{{\rm d}V}\right] { \rm d}V
\end{displaymath}](img7239.gif)
![]()
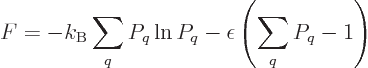
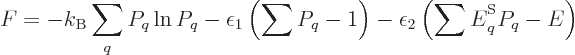
![]()
![]()
![]() ,
,