|
|
|
|
|
Next: N.11 Better description of two-state systems |
|
This note gives a simple model for the emission of a particle like a
photon. It is assumed that the emitted particle has a typical quantum
wave length ![]()
![]()
First, photon wave functions are messy and not that easy to make sense
of, {A.21.7}. The photon would be much simpler if it did
not have spin and was nonrelativistic. A reasonable wave function for
a hypothetical spinless nonrelativistic photon coming out of the
center of the emitter with typical wave length ![]()
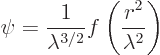
The above wave function has no preferred direction in the emission,
making it spherically symmetric. It depends only on the distance ![]()
![]() ,
,
There are various reasons to give why you would want the wave function of a particle coming out of the origin to have zero angular momentum. For one, since it comes out of a featureless point, there should not be a preferred direction. Or in terms of classical physics, if it had angular momentum then it would have to have infinite velocity at the origin. The similar quantum idea is that the relevant wave functions for a particle moving away from the origin, the Hankel functions of the first kind, blow up very strongly at the origin if they have angular momentum, {A.6}. But it is really better to describe the emitted particle in terms of the Bessel functions of the first kind. These have zero probability of the particle being at the origin if the angular momentum is not zero. And a particle should not be created at a point where it has zero probability of being.
Of course, a spherically symmetric quantum wave function also means
that the particle is moving away from the emitter equally in all
directions. Following the stated ideas of quantum mechanics, this
will be true until the position of the particle is
measured.
Any macroscopic surroundings cannot
reasonably remain uncommitted to exactly where the outgoing particle
is for very long.
Now consider the same sort of emission, but from a point in the
emitter a bit away from the center. For simplicity, assume the
emission point to be at ![]() ,
,![]()
![]()
![]() -
-
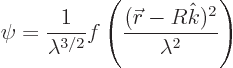
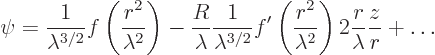
That makes the probability for ![]()
![]()
![]() .
.![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]() .
.