| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.84 Band gap explanation derivations
To see mathematically how the results of note {N.9}
were obtained requires knowledge of linear algebra. If you are
unaware of it, definitely skip the below derivation.
First define the “growth matrix  that gives the values of
that gives the values of
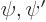 at
at 

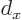 given the values at
given the values at 
 0:
0:
Simply take the initial conditions to be 1,0 and 0,1 respectively, and
find the solutions at 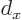 to find the two columns of
to find the two columns of  .
.
Since the potential is the same in all atomic cell, matrix  describes the change over any cell, not just the first one. And for a
periodic solution for a box with
describes the change over any cell, not just the first one. And for a
periodic solution for a box with 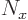
atoms,
after
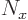 applications of
applications of  the original values of
the original values of 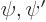 must be
obtained. According to linear algebra, and assuming that the two
eigenvalues of
must be
obtained. According to linear algebra, and assuming that the two
eigenvalues of  are unequal, that means that at least one
eigenvalue of
are unequal, that means that at least one
eigenvalue of  raised to the power
raised to the power 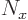 must be 1.
must be 1.
Now matrix  must have unit determinant, because for the two basic
solutions with 1,0 and 0,1 initial conditions,
must have unit determinant, because for the two basic
solutions with 1,0 and 0,1 initial conditions,
for all  . The quantity in the left hand side is called the
Wronskian of the solutions. To verify that it is indeed constant,
take
. The quantity in the left hand side is called the
Wronskian of the solutions. To verify that it is indeed constant,
take 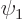 times the Hamiltonian eigenvalue problem for
times the Hamiltonian eigenvalue problem for 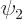 minus
minus 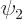 times the one for
times the one for 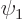 to get
to get
According to linear algebra, if  has unit determinant then the
product of its two eigenvalues is 1. Therefore, if its eigenvalues
are unequal and real, their magnitude is unequal to 1. One will be
less than 1 in magnitude and the other greater than 1. Neither can
produce 1 when raised to the power
has unit determinant then the
product of its two eigenvalues is 1. Therefore, if its eigenvalues
are unequal and real, their magnitude is unequal to 1. One will be
less than 1 in magnitude and the other greater than 1. Neither can
produce 1 when raised to the power 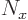 , so there are no
periodic solutions. Energies that produce such matrices
, so there are no
periodic solutions. Energies that produce such matrices  are in
the band gaps.
are in
the band gaps.
If the eigenvalues of  are complex conjugates, they must have
magnitude 1. In that case, the eigenvalues can always be written in
the form
are complex conjugates, they must have
magnitude 1. In that case, the eigenvalues can always be written in
the form
for some value of 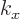 . For either eigenvalue raised to
the power
. For either eigenvalue raised to
the power 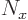 to produce 1,
to produce 1, 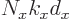 must be a whole multiple of
must be a whole multiple of
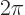 . That gives the same wave number values as for the
free-electron gas.
. That gives the same wave number values as for the
free-electron gas.
To see when the eigenvalues of  have the right form, consider the
sum of the eigenvalues. This sum is called the trace. If the
eigenvalues are real and unequal, and their product is 1, then the
trace of
have the right form, consider the
sum of the eigenvalues. This sum is called the trace. If the
eigenvalues are real and unequal, and their product is 1, then the
trace of  must be greater than 2 in magnitude. (One way of seeing
that for positive eigenvalues is to multiply out the expression
must be greater than 2 in magnitude. (One way of seeing
that for positive eigenvalues is to multiply out the expression
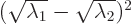
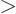 0. For negative ones, add two
minus signs in the square roots.) Conversely, when the eigenvalues
are complex conjugates, their sum equals
0. For negative ones, add two
minus signs in the square roots.) Conversely, when the eigenvalues
are complex conjugates, their sum equals 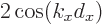 according to
the Euler formula (2.5). That is less than 2 in magnitude.
So the condition for valid periodic eigenfunctions becomes
according to
the Euler formula (2.5). That is less than 2 in magnitude.
So the condition for valid periodic eigenfunctions becomes
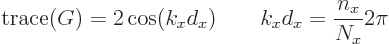
From the fact that periodic solutions with twice the crystal period
exist, (the ones at the band gaps), it is seen that the values of the
trace must be such that the cosine runs through the entire gamut of
values. Indeed when the trace is plotted as a function of the energy,
it oscillates in value between minima less than -2 and maxima greater
than 2. Each segment between adjacent minima and maxima produces one
energy band. At the gap energies
because the cosine is at its 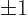 extrema at the gap energies. So
the velocity becomes zero at the ends of the bands.
extrema at the gap energies. So
the velocity becomes zero at the ends of the bands.
Identification of the eigenfunctions using the growth matrix  is
readily put on a computer. A canned zero finder can be used to find
the energies corresponding to the allowed values of the trace.
is
readily put on a computer. A canned zero finder can be used to find
the energies corresponding to the allowed values of the trace.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
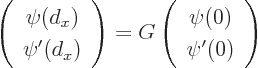
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
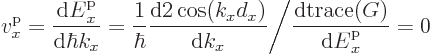
![]()