|
|
|
|
|
Next: 6.16 Chemical Potential and Diffusion |
|
The valence electrons in a block of metal have tremendous kinetic
energy, of the order of electron volts. These electrons would like to
escape the confines of the block, but attractive forces exerted by the
nuclei hold them back. However, if the temperature is high enough,
typically 1 000 to 2 500 K, a few electrons can pick up enough
thermal energy to get away. The metal then emits a current of
electrons. This is called thermionic emission.
It is
important for applications such as electron tubes and fluorescent
lamps.
The amount of thermionic emission depends not just on temperature, but
also on how much energy electrons inside the metal need to escape.
Now the energies of the most energetic electrons inside the metal are
best expressed in terms of the Fermi energy level. Therefore, the
energy required to escape is conventionally expressed relative to that
level. In particular, the additional energy that a Fermi-level
electron needs to escape is traditionally written in the form
![]()
![]()
![]()
The thermionic emission equation gives the current density of
electrons as, {D.29},
| (6.23) |
Note that thermionic emission depends exponentially on the temperature; unless the temperature is high enough, extremely little emission will occur. You see the Maxwell-Boltzmann distribution at work here. This distribution is applicable since the number of electrons per state is very small for the energies at which the electrons can escape.
Despite the applicability of the Maxwell-Boltzmann distribution,
classical physics cannot explain thermionic emission. That is seen
from the fact that the constant ![]()
![]() .
.
Thermionic emission can be helped along by applying an additional
electric field ![]()
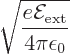 |
(6.24) |
tunnelout due to their quantum uncertainty in position. That is called “field emission.” It depends exponentially on the field strength, which must be very high as the quantum uncertainty in position is small.
It may be noted that the term thermionic emission
may
be used more generally to indicate the flow of charge carriers, either
electrons or ions, over a potential barrier. Even for standard
thermionic emission, it should be cautioned that the work function
depends critically on surface conditions. For example, surface
pollution can dramatically change it.
Key Points
- Some electrons can escape from solids if the temperature is sufficiently high. That is called thermionic emission.
- The work function is the minimum energy required to take a Fermi-level electron out of a solid, per unit charge.
- An additional electric field can help the process along, in more ways than one.