| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.29 The thermionic emission equation
This note derives the thermionic emission equation for a typical metal
following [42, p. 364ff]. The derivation is semi-classical.
To simplify the analysis, it will be assumed that the relevant
electrons in the interior of the metal can be modeled as a
free-electron gas. In other words, it will be assumed that in the
interior of the metal the forces from surrounding particles come from
all directions and so tend to average out.
(The free-electron gas assumption is typically qualitatively
reasonable for the valence electrons of interest if you define the
zero of the kinetic energy of the gas to be at the bottom of the
conduction band. You can also reduce errors by replacing the true
mass of the electron by some suitable effective mass.
But the zero of the energy drops out in the final expression, and the
effective mass of typical simple metals is not greatly different from
the true mass. See chapter 6.22.3 for more on these issues.)
Assume that the surface through which the electrons escape is normal
to the  -direction. Then the classical expression for the current
of escaping electrons is
-direction. Then the classical expression for the current
of escaping electrons is
where 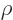 is the number of electrons per unit volume that is
capable of escaping and
is the number of electrons per unit volume that is
capable of escaping and  is their velocity in the
is their velocity in the
 -direction. Note that the current above is supposed to be
the current inside the metal of the electrons that will escape.
-direction. Note that the current above is supposed to be
the current inside the metal of the electrons that will escape.
An electron can only escape if its energy 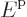 exceeds
exceeds
where 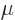 is the Fermi level, because the work function
is the Fermi level, because the work function 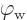 is defined that way. The number of electrons per unit volume in an
energy range
is defined that way. The number of electrons per unit volume in an
energy range 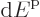 above
above 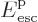 can be found as
can be found as
That is because the initial exponential is a rewritten
Maxwell-Boltzmann distribution (6.21) that gives the number
of electrons per state, while the remainder is the number of
states in the energy range according to the density of states
(6.6).
Normally, the typical thermal energy  is very small compared
to the minimum energy
is very small compared
to the minimum energy 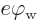 above the Fermi level needed to
escape. Then the exponential of the Maxwell-Boltzmann distribution is
very small. That makes the amount of electrons with sufficient energy
to escape very small. In addition, with increasing energy above
above the Fermi level needed to
escape. Then the exponential of the Maxwell-Boltzmann distribution is
very small. That makes the amount of electrons with sufficient energy
to escape very small. In addition, with increasing energy above
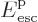 the amount of electrons very quickly becomes much
smaller still. Therefore only a very small range of energies above
the minimum energy
the amount of electrons very quickly becomes much
smaller still. Therefore only a very small range of energies above
the minimum energy 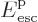 gives a contribution.
gives a contribution.
Further, even if an electron has in principle sufficient energy to
escape, it can only do so if enough of its momentum is in the
 -direction. Only momentum that is in the
-direction. Only momentum that is in the  -direction can be used
to overcome the nuclei that pull it back towards the surface when it
tries to escape. Momentum in the other two directions only produces
motion parallel to the surface. So only a fraction, call it
-direction can be used
to overcome the nuclei that pull it back towards the surface when it
tries to escape. Momentum in the other two directions only produces
motion parallel to the surface. So only a fraction, call it
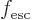 , of the electrons that have in principle enough
energy to escape can actually do so. A bit of geometry shows how
much. All possible end points of the momentum vectors with a
magnitude
, of the electrons that have in principle enough
energy to escape can actually do so. A bit of geometry shows how
much. All possible end points of the momentum vectors with a
magnitude 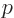 form a spherical surface with area
form a spherical surface with area 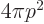 .
But only a small circle on that surface around the
.
But only a small circle on that surface around the  -axis, with an
approximate radius of
-axis, with an
approximate radius of  , has enough
, has enough
 -momentum for the electron to escape, so
-momentum for the electron to escape, so
where the final equality applies since the kinetic energy is
proportional to the square momentum.
Since the velocity for the escaping electrons is mostly in the
 -direction,
-direction, 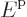
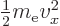 , which can be
used to express
, which can be
used to express  in terms of energy.
in terms of energy.
Putting it all together, the current density becomes
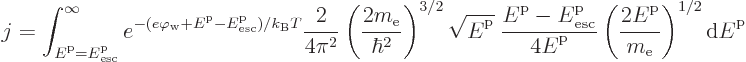
Rewriting in terms of a new integration variable
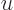

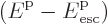

 gives the thermionic emission
equation.
gives the thermionic emission
equation.
If an external electric field 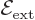 helps the electrons
escape, it lowers the energy that the electrons need to do so.
Consider the potential energy in the later stages of escape, at first
still without the additional electric field. When the electron looks
back at the metal surface that it is escaping from, it sees a positron
mirror image of itself inside the metal. Of course, there is not
really a positron inside the metal; rearrangement of the surface
electrons of the metal create this illusion. The surface electrons
rearrange themselves to make the total component of the electric field
in the direction parallel to the surface zero. Indeed, they have to
keep moving until they do so, since the metal has negligible
electrical resistance in the direction parallel to the surface. Now
it just so happens that a positron mirror image of the electron has
exactly the same effect as this rearrangement. The escaping electron
pushes the surface electrons away from itself; that force has a
repulsive component along the surface. The positron mirror image
however attracts the surface electrons towards itself, exactly
cancelling the component of force along the surface exerted by the
escaping electron.
helps the electrons
escape, it lowers the energy that the electrons need to do so.
Consider the potential energy in the later stages of escape, at first
still without the additional electric field. When the electron looks
back at the metal surface that it is escaping from, it sees a positron
mirror image of itself inside the metal. Of course, there is not
really a positron inside the metal; rearrangement of the surface
electrons of the metal create this illusion. The surface electrons
rearrange themselves to make the total component of the electric field
in the direction parallel to the surface zero. Indeed, they have to
keep moving until they do so, since the metal has negligible
electrical resistance in the direction parallel to the surface. Now
it just so happens that a positron mirror image of the electron has
exactly the same effect as this rearrangement. The escaping electron
pushes the surface electrons away from itself; that force has a
repulsive component along the surface. The positron mirror image
however attracts the surface electrons towards itself, exactly
cancelling the component of force along the surface exerted by the
escaping electron.
The bottom line is that it seems to the escaping electron that it is
pulled back not by surface charges, but by a positron mirror image of
itself. Therefore, including now an additional external electrical
field, the total potential in the later stages of escape is:
where 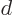 is the distance from the surface. The first term is the
attracting force due to the positron image, while the second is due to
the external electric field. The constant depends on where the zero
of energy is defined. Note that only half the energy of attraction
between the electron and the positron image should be assigned to the
electron; the other half can be thought of as
is the distance from the surface. The first term is the
attracting force due to the positron image, while the second is due to
the external electric field. The constant depends on where the zero
of energy is defined. Note that only half the energy of attraction
between the electron and the positron image should be assigned to the
electron; the other half can be thought of as work
on
the image. If that is confusing, just write down the force on the
electron and integrate it to find its potential energy.
If there is no external field, the maximum potential energy that the
electron must achieve occurs at infinite distance 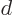 from the metal
surface. If there is an electric field, it lowers the maximum
potential energy, and it now occurs somewhat closer to the surface.
Setting the derivative of
from the metal
surface. If there is an electric field, it lowers the maximum
potential energy, and it now occurs somewhat closer to the surface.
Setting the derivative of  with respect to
with respect to 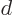 to zero to identify
the maximum, and then evaluating
to zero to identify
the maximum, and then evaluating  at that location shows that the
external field lowers the maximum potential energy that must be
achieved to escape by
at that location shows that the
external field lowers the maximum potential energy that must be
achieved to escape by 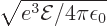 .
.
![]() -
-![]()

![]()
![]()
![]()
![]()
![]() -
-![]() -
-![]() ,
,![]()
![]() .
.![]() -
-![]() ,
,![]() -
-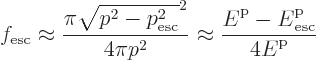
![]() -
-![]()
![]()
![]() ,
,![]()
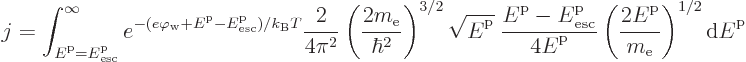
![]()
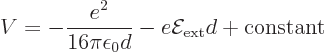
![]()
![]()
![]()
![]()
![]() .
.