|
|
|
|
|
Next: 6.12 Confinement and the DOS |
|
According to the previous sections, electrons, being fermions, behave in a way very differently from bosons. A system of bosons has very little energy in its ground state, as all bosons collect in the spatial state of lowest energy. Electrons cannot do so. At most two electrons can go into a single spatial state. A macroscopic system of electrons must occupy a gigantic number of states, ranging from the lowest energy state to states with many orders of magnitude more energy.
As a result, a free-electron gas
of ![]()
![]() .
.
Having so much kinetic energy, the electrons exert a tremendous
pressure on the walls of the container that holds them. This pressure
is called degeneracy pressure.
It explains
qualitatively why the volume of a solid or liquid does not collapse
under normally applied pressures.
Of course, degeneracy pressure is a poorly chosen name. It is really
due to the fact that the energy distribution of electrons is
not degenerate, unlike that of bosons. Terms like
exclusion-principle pressure
or “Pauli
pressure” would capture the essence of the idea. So they are
not acceptable.
The magnitude of the degeneracy pressure for a free-electron gas is
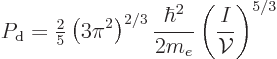 |
(6.18) |
A ballpark number for the degeneracy pressure is very instructive.
Consider once again the example of a block of copper, with its valence
electrons modeled as a free-electron gas, Using the same numbers as in
the previous section, the degeneracy pressure exerted by these valence
electrons is found to be 40 1![]()
This tremendous outward pressure is balanced by the nuclei that pull on electrons that try to leave the block. The details are not that simple, but electrons that try to escape repel other, easily displaced, electrons that might aid in their escape, leaving the nuclei unopposed to pull them back. Obviously, electrons are not very smart.
It should be emphasized that it is not mutual repulsion of the electrons that causes the degeneracy pressure; all forces on the electrons are ignored in the interior of the block. It is the uncertainty relationship that requires spatially confined electrons to have momentum, and the exclusion principle that explodes the resulting amount of kinetic energy, creating fast electrons that are as hard to contain as students on the day before Thanksgiving.
Compared to a 1![]()
![]()
However, under extremely high pressures, the electron pressure can
lose out. In particular, for neutron stars the spatial electron
states collapse under the very weight of the massive star. This is
related to the fact that the degeneracy pressure grows less quickly
with compression when the velocity of the electrons becomes
relativistic. (For very highly relativistic particles, the kinetic
energy is not given in terms of the momentum ![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
Key Points
- Because typical confined electrons have so much kinetic energy, they exert a great degeneracy pressure on what is holding them.
- This pressure makes it very hard to compress liquids and solids significantly in volume.
- Differently put, liquids and solids are almost incompressible under typical conditions.