|
|
|
|
|
Next: 10.7 Additional Points |
|
The free-electron energy spectrum does not have bands. Bands only form when some of the forces that the ambient solid exerts on the electrons are included. In this section, some of the mechanics of that process will be explored. The only force considered will be one given by a periodic lattice potential. The discussion will still ignore true electron-electron interactions, time variations of the lattice potential, lattice defects, etcetera.
In addition, to simplify the mathematics it will be assumed that the lattice potential is weak. That makes the approach here diametrically opposite to the one followed in the discussion of the one-dimensional crystals. There the starting point was electrons tightly bound to widely spaced atoms; the atom energy levels then corresponded to infinitely concentrated bands that fanned out when the distance between the atoms was reduced. Here the starting idea is free electrons in closely packed crystals for which the bands are completely fanned out so that there are no band gaps left. But it will be seen that when a bit of nontrivial lattice potential is added, energy gaps will appear.
The analysis will again be based on the Floquet energy eigenfunctions
for the electrons. As noted in the previous section, they correspond
to periodic boundary conditions for periods ![]() ,
,![]() ,
,![]() .
.![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() .
.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(400,19...
...0)[t]{$k_x$}}
\put(-2,187){\makebox(0,0)[r]{$k_y$}}
\end{picture}
\end{figure}](img2238.gif) |
The approach will be to start with the solutions for force-free
electrons and see how they change if a small, but nonzero lattice
potential is added to the motion. It will be a “nearly-free electron model.” Consider a sample Floquet
wave number as shown by the red dot in the wave number space figure
10.20. If there is no lattice potential, the
corresponding energy eigenfunction is the free-electron one,
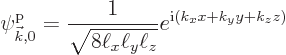
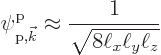
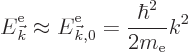
However, that is not good enough. The interest here is in the changes in the energy due to the lattice potential, even if they are weak. So the first thing will be to figure out these energy changes.
Finding the energy changes due to a small change in a Hamiltonian can be done by a mathematical technique called “perturbation theory.” A full description and derivation are in {A.38} and {D.79}. This subsection will simply state the needed results.
The effects of a small change in a Hamiltonian, here being the weak
lattice potential, are given in terms of the so-called
Hamiltonian perturbation coefficients
defined as
| (10.13) |
In those terms, the energy of the eigenfunction ![]()
![]()
The first correction to the free-electron energy is the Hamiltonian
perturbation coefficient ![]() .
.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(400,19...
...0)[t]{$k_x$}}
\put(-2,187){\makebox(0,0)[r]{$k_y$}}
\end{picture}
\end{figure}](img2249.gif) |
That makes the sum in (10.14) the physically interesting
change in energy. Now, unlike it seems from the given expression, it
is not really necessary to sum over all free-electron energy
eigenfunctions ![]() .
.![]()
![]()
![]()
The correct expression for the energy change has therefore now been
identified. There is one caveat in the whole story, though. The
above analysis is not justified if there are eigenfunctions
![]()
![]()
![]() .
.
Fortunately, since the grid is so widely spaced, the problem occurs
only for relatively few energy eigenfunctions ![]() .
.![]()
![]()
![]()
![]() ,
,![]()
![]() .
.![]()
![]() .
.![]()
The previous subsection determined how the energy changes from the
free-electron gas values due to a small lattice potential. It was
found that an energy level ![]()
The expression above for the energy change is not valid when
![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
One case for which this happens is when the wave number vector ![]()
![]()
![]()
![]()
For the left of the two states, ![]()
![]() ,
,![]()
![]() ,
,
 |
That is illustrated for an arbitrarily chosen example lattice potential in figure 10.23. It is another reason why the Wigner-Seitz cell around the origin, i.e. the first Brillouin zone, is particularly important. For different lattices than the simple cubic one considered here, it is still the distance from the origin that is the deciding factor, so in general, it is the Wigner-Seitz cell, rather than some parallelepiped-shaped primitive cell along whose surfaces the energies get torn apart.
But notice in figure 10.23 that the energy levels get torn
apart along many more surfaces than just the surface of the first
Brillouin zone. In general, it can be seen that tears occur in wave
number space along all the perpendicular bisector planes, or Bragg planes, between the points of the reciprocal lattice and the
origin. Figure 10.24 shows their intersections with the
cross section ![]()
![]()
![]()
![]()
Recall that the Bragg planes are also the boundaries of the fragments that make up the various Brillouin zones. In fact the first Brillouin zone is the cube or Wigner-Seitz cell around the origin; (the square around the origin in the cross section figure 10.24). The second zone consists of six pyramid-shaped regions whose bases are the faces of the cube; (the four triangles sharing a side with the square in the cross section figure 10.24). They can be pushed into the first Brillouin zone using the fundamental translation vectors to combine into a Wigner-Seitz cell shape.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,16...
...)[t]{$k_x$}}
\put(102,156){\makebox(0,0)[r]{$k_y$}}
\end{picture}
\end{figure}](img2261.gif) |
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,51...
...)[t]{$k_x$}}
\put(102,156){\makebox(0,0)[r]{$k_y$}}
\end{picture}
\end{figure}](img2262.gif) |
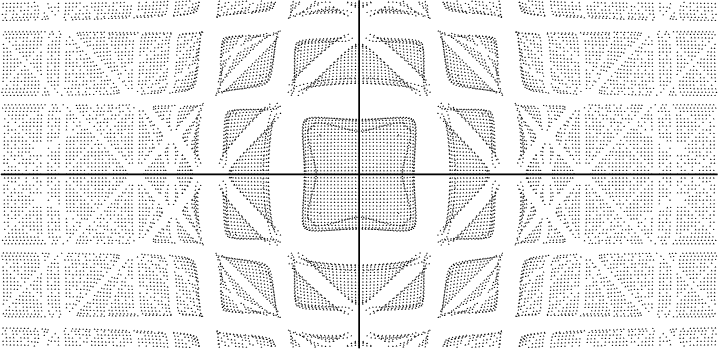
For a sufficiently strong lattice potential like the one in figure
10.23, the energy levels in the first Brillouin zone, the
center patch, are everywhere lower than in the remaining areas.
Electrons will then occupy these states first, and since there are
![]()
The wave number space in the right half of figure 10.25 also illustrates that a lattice potential can change the Floquet wave number vectors that get occupied. For the free-electron gas, the occupied states formed a spherical region in terms of the wave number vectors, as shown in the middle of figure 10.17, but here the occupied states have become a cube, the Wigner-Seitz cell around the origin. The Fermi surface seen in the extended zone scheme is now no longer a spherical surface, but consists of the six faces of this cell.
But do not take this example too literally: the small-perturbation
analysis is invalid for the strong potential required for an
insulator, and the real picture would look quite different. In
particular, the roll-over
of the states at the edge of
the first Brillouin zone in the energy plot is a clear indication that
the accuracy is poor. The error in the perturbation analysis is the
largest for states immediately next to the Bragg planes. The example
is given just to illustrate that the nearly-free electron model can
indeed describe band gaps if taken far enough.
The nearly-free electron model is more reasonable for the smaller lattice forces experienced by valence electrons in metals. For example, at reduced strength, the same potential as before produces figure 10.26. Now the electrons have no trouble finding states of slightly higher energy, as it should be for a metal. Note, incidentally, that the Fermi surfaces in the right-hand graphs seem to meet the Bragg planes much more normally than the spherical free-electron surface. That leads to smoothing out of the corners of the surface seen in the periodic zone scheme. For example, imagine the center zone of the one valence electron wave number space periodically continued.