| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
4.3.3.3 Solution hydc-c
Question:
Based on the results of the previous question, what is the color of the light emitted in a Balmer transition from energy  to
to 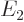 ? The Planck-Einstein relation says that the angular frequency
? The Planck-Einstein relation says that the angular frequency 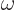 of the emitted photon is its energy divided by
of the emitted photon is its energy divided by 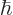 , and the wave length of light is
, and the wave length of light is 

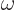 where
where  is the speed of light. Typical wave lengths of visible light are: violet 400 nm, indigo 445 nm, blue 475 nm, green 510 nm, yellow 570 nm, orange 590 nm, red 650 nm.
is the speed of light. Typical wave lengths of visible light are: violet 400 nm, indigo 445 nm, blue 475 nm, green 510 nm, yellow 570 nm, orange 590 nm, red 650 nm.
Answer:
The energy carried away by the photon is the energy lost by the electron, which is
Dividing by 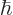
 1.054 10
1.054 10 J s gives the angular frequency to be 2.87 10
J s gives the angular frequency to be 2.87 10 /s, and then the wave length is 656 nm, using
/s, and then the wave length is 656 nm, using 
 3 10
3 10 m/s. That will be red light.
m/s. That will be red light.
![]()
![]() ?
?![]()
![]() ,
,![]()
![]()
![]()
![]()
