8.2.7 Comparison with boundary layer theory

In this section we will compare our results to some of the predictions of boundary layer theory. Boundary layer theory is based on the approximation that the Reynolds number is large.

According to this theory, the first significant development is the formation of flow reversal. This was already pointed out during the initial discovery of boundary layers by Prandtl [176]. The theoretical description of the flow reversal process was given by Blasius [26]. He found that for the impulsively started circular cylinder, flow reversal occurs very quickly. The best current estimate for the time of flow reversal is probably $t=0.32192$ as given by Cowley [69]. At this time the cylinder has moved over a distance of no more than a sixth of its diameter. The reversed flow first appears at the rear stagnation point, and spreads upstream from that point to rapidly cover most of the rear cylinder surface.

Our numerical results are in excellent agreement with the predictions of boundary layer theory for flow reversal. For example, figure 8.13 compares our velocity profiles at $Re=9,500$ with the boundary layer predictions. We show both the standard boundary layer results (or first order theory), which are valid for infinite Reynolds number, as well as second order theory, which attempts to correct for the finite Reynolds number. Note that second order boundary layer theory does present a noticeable improvement above the standard boundary layer results. (The boundary layer profiles are unpublished Eulerian results of Van Dommelen & Shankar and are highly accurate; for example, the first flow reversal is found at $t=0.32194$ versus $0.32192$.)

Close examination of the velocity profile located 150 degrees from the front symmetry plane shows that reversed flow has already penetrated beyond this station. Excellent agreement between our numerical results and boundary layer theory also exists at the rear stagnation point, figure 8.31.

Flow reversal is quite a distinctive process. At time $t=0.32192$, all of the following occur:

1. The first flow reversal at the rear stagnation point.

2. The first formation of a point of zero wall shear on the cylinder surface away from the symmetry lines. This point is located at the upstream limit of the region of reversed flow.

3. The first formation of a point of zero vorticity on the cylinder surface away from the symmetry lines. This point coincides with the point of zero wall shear.

4. The first bifurcation of the wall streamline at a point away from the symmetry lines. This point too coincides with the point of zero wall shear.

5. The first formation of `recirculating eddies': streamlines that close on themselves. Although in an unsteady flow the streamlines do not indicate the true geometry of the path lines followed by the fluid, still the streamline picture is easily visualized experimentally and appealing.

6. The formation of the first internal stagnation points in the interior of the fluid, as the points around which the closed streamlines `circulate'.

However, despite all these interesting features, the time $t=0.32192$ of first flow reversal is at present no longer considered to be of great physical importance. In the early days of boundary layer theory, it was believed that flow reversal would indicate a significant motion of the boundary layer vorticity away from the wall, called `flow separation'. However, it has become clear in the last quarter century that this is only true for steady flows. For unsteady flows, the true separation process occurs at a second and later time, through an additional flow development which is now generally known as the `Van Dommelen & Shen singularity.'

We should note that some authors still mistakenly use the term `separation' to indicate flow reversal in unsteady flow. This is unfortunate, because since the very beginning of boundary layer theory `separation' was intended to mean an actual significant separation of the boundary layer away from the wall. For example, both Prandtl [176] and Blasius [26] described separation as a penetration of the boundary layer away from the wall, large enough to `completely alter' the flow and invalidate the boundary layer solutions.

Yet a large number of numerical computations have shown that the boundary layer solution can be continued for at least some time beyond the first flow reversal. This implies that for high Reynolds numbers the boundary layer must still be thin, proportional to $1/\sqrt{Re}$, and aligned along the surface. Our numerical computations indicate that this is indeed the case. Even at a time as large as $t=1$ (three times the flow reversal time), the boundary layer is very thin and smooth, especially at the higher Reynolds numbers. We refer to our vorticity fields in figures 8.18 and 8.19.

Historically, it took long before it was truly recognized that flow reversal does not necessarily indicate a significant thickening of unsteady boundary layers. In fact, this fact was first clearly noted in about the late 1950's, most notably by Moore [160], Rott [187], and Sears [197].

Expanding on the earlier work by Moore [160], Sears & Telionis [196] hypothesized that there might be a second point, different from the point of zero wall shear at which a boundary layer truly separates from the wall. This second point would then define the actual physical separation point. The first example of such a separation point was discovered numerically by Van Dommelen & Shen [243]. They found that for the impulsively started circular cylinder at infinite Reynolds number, it occurs at time $t=1.502$, at symmetric angular positions 69 degrees from the rear symmetry line. Cowley [69] independently reached these conclusions from a high-order small time expansion of the flow.

The correct structure of this separation process was also first discovered by Van Dommelen & Shen, in a different paper [241]. They found that for sufficiently high Reynolds number, it takes the form of a local thickening of the boundary layer. This thickening should become relatively more pronounced at higher Reynolds numbers, since the unseparated boundary layer thickness thins somewhat more quickly than the separating one when the Reynolds number is increased.

Unfortunately, the Reynolds numbers in the current computations are too low to expect a very close agreement with the solution at infinite Reynolds number. This may be particularly true for a circular cylinder, in which even the unseparated boundary layer at the rear is quite thick. In addition, theoretical results of Elliot, Cowley & Smith [77] suggest that the Reynolds number might well have to be as large $10^{22}$ for an accurate agreement with theory. Yet, our results for the higher Reynolds numbers 9,500 and 20,000 do clearly show that local boundary layer thickening occurs at roughly the predicted time $t=1.5$.

Figure 8.37: Impulsively translated cylinder: (a) Local vorticity contours obtained from the Van Dommelen & Shen singularity [241]; (b) and (c) local vorticity fields at $t=1.50$ for $Re=9,500$ and $Re=20,000$ obtained from the vorticity redistribution method.

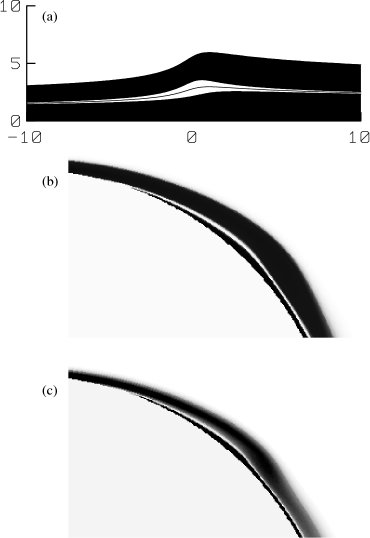The local form of the vorticity field as predicted by the theory of Van Dommelen and Shen [241] is shown in figure 8.37(a). This figure uses scaled local coordinates, in which the vertical scaling is generally different from the horizontal one. The mathematical form of this local vorticity field is a complex expression involving incomplete elliptic integrals and need not concern us here. The most important property is that the thickening is due to a local accumulation of fluid particles on the vorticity reversal line in the middle of the boundary layer.

A close examination of our computed vorticity fields at Reynolds numbers 9,500 and 20,000 at times near $t=1.50$ shows good qualitative agreement with this asymmetric local expansion of the region of reversing vorticity within the boundary layer. Magnified local boundary layer regions are shown in figures 8.37(b) and (c); they were taken from figures 8.18 and 8.19, converted to monochrome and contrast enhanced. It seems clear that the boundary layer theory remains meaningful even at Reynolds numbers as low as those in the present study.

Current boundary layer theory cannot yet predict what happens after the local thickening has developed. However, the fact that the upper part of the boundary layer develops into a free shear layer [242], as well as experimental data [222] suggest that the boundary layer vorticity may roll up into a discrete vortex [242]. The process would be similar to a Kelvin-Helmholtz instability. This seems in excellent agreement with our results for the higher Reynolds numbers, figures 8.18 and 8.19.

We also note that the initiation time of this vortex does seem to converge towards the time $t=1.50$ predicted by theory; compare the results of figure 8.18 to those of 8.19. However, the locations of the thickening and the vortex do seem noticeably different from the value of 69 degrees from the rear symmetry plane valid for infinite Reynolds number. Yet, for our relatively low Reynolds numbers the agreement with theory is still excellent.