5 Processes

5.1 Control Mass Processes (Closed Systems)

Specific heat and work:

$$q_{12} = \frac{Q_{12}}{m} \quad w_{12} = \frac{W_{12}}{m} \qquad Q_{12} = m\; q_{12} \quad W_{12} = m\; w_{12}$$

Continuity (mass conservation):

$$m_1 \left(+ m_{\mbox{\scriptsize added}} \right) = m_2$$

The first law of thermo (energy conservation):

$$E_2 - E_1 = Q_{12} - W_{12} \qquad (E = U + m {\textstyle \frac12}{\bf V}^2? + m g z?)$$

Work:

$$W_{12} = \int_1^2 p \; {\rm d} V = \left\{ \begin{arra... ...1}} pV\ln\left(\frac{V_2}{V_1}\right) \end{array} \right.$$

In case of an ideal gas, note that $pV$ can be replaced by $mRT$.

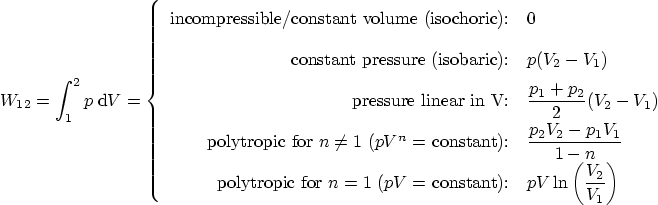
No heat is added or removed if the process is adiabatic.
Exams 3 and final only
More generally:

$$Q_{12} = \left\{ \begin{array}{rl} \mbox{Adiabatic:}... ...tyle\vphantom{\int_1^2} T (S_2-S_1) \end{array} \right.$$

The second law for reversible adiabatic (isentropic) processes:

$$S_2 = S_1$$

The second law of thermo for general processes:

$$S_{12,\mbox{\scriptsize gen}} + \sum \frac{Q_{k}}{T_{k}} = S_2 - S_1 \qquad S_{12,\mbox{\scriptsize gen}} \ge 0$$

End exams 3 and final only

5.2 Rate Equations

The first law as a rate equation:

$$\frac{{\rm d}E}{{\rm d}t} = \dot Q - \dot W \qquad \left... ...bf V}^2}{{\rm d}t}? + m g \frac{{\rm d}Z}{{\rm d}t}?\right)$$

Work as a rate equation:

$$\dot W = p \dot V$$

For an ideal gas:

$$\frac{{\rm d}u}{{\rm d}t} = C_v \frac{{\rm d}T}{{\rm d}t}$$

For liquids and solids:

$$\dot Q = m C_{(p)} \frac{{\rm d}T}{{\rm d}t}$$

5.3 Steady State Control Volume Processes

The control volume is assumed to be steady state in all formulae below.

Specific work output and heat added (i.e., per unit mass flowing through):

$$w = \frac{\dot W}{\dot m} \quad q = \frac{\dot Q}{\dot m} \qquad \dot W = \dot m w \quad \dot Q = \dot m q$$

In- and outflow velocities and pipe cross-sectional areas:

$$\dot m = \dot V/v = A {\bf V}/v \qquad A=\frac\pi 4 D^2$$

(where ${\bf V}$ is velocity.)

Continuity (mass conservation):

$$\sum \dot m_i = \sum \dot m_e$$

where $\sum$ means sum over all inflow, respectively outflow, points, if there is more than one.

The first law of thermo (energy conservation):

$$\sum \dot m_e \left(h_e+ \frac12 {\bf V}_e^2 + g z_e\right... ...t(h_i+ \frac12 {\bf V}_i^2 + g z_i\right) = \dot Q - \dot W$$

The kinetic energy and potential energy terms are often ignored. Devices without moving parts do not do work, $\dot W = 0$. Adiabatic devices have no heat transfer, $\dot Q = 0$.

Exams 3 and final only

The second law of thermo for a reversible adiabatic (isentropic) process inside a single entrance and exit CV:

$$s_e = s_i$$

The second law of thermo for a reversible isothermal process inside a single entrance and exit CV:

$$q = T \left(s_e - s_i\right)$$

The second law for a general control volume:

$$\sum \dot m_e s_e - \sum \dot m_i s_i = \sum \frac{\dot ... ...riptsize gen}} \qquad \dot S_{\mbox{\scriptsize gen}} \ge 0$$

Specific work done during a reversible process inside a single entrance and exit CV:

$$w + {\textstyle \frac12} {\bf V}_e^2? - {\textstyle \frac12} {\bf V}_i^2? + g Z_e? - g Z_i? = - \int_i^e v \; {\rm d} p$$

where

$$- \int_i^e v \; {\rm d} p = \left\{ \begin{array}{rl} ... ...- p v \ln\left(\frac{p_e}{p_i}\right) \end{array} \right.$$

In case of an ideal gas, note that $pv$ can be replaced by $RT$.

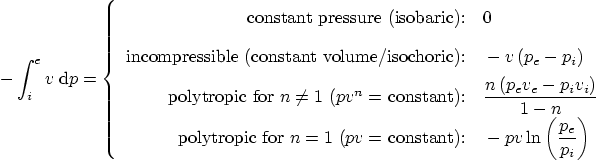
Special case of (a) ideal gas, (2) polytropic, $n\ne 1$, (including isentropic constant specific heats, then $n=k$,) and (3) reversible:

$$- \int_i^e v \; {\rm d} p = \frac{nRT_1}{1-n}\left[\left(\frac{P_2}{P_1}\right)^{(n-1)/n}-1\right]$$

Special case of (a) ideal gas, (2) constant specific heats, (3) polytropic, $n=1$ (isothermal). and (4) reversible:

$$- \int_i^e v \; {\rm d} p = -RT\ln\frac{P_2}{P_1}$$

Adiabatic turbine and compressor/pump efficiencies:

$$\eta_{\mbox{\scriptsize T}} = \frac{w_a}{w_s} \qquad \eta_{\mbox{\scriptsize C}} = \frac{w_s}{w_a}$$

where subscript $s$ indicates an ideal isentropic device with the same entrance conditions and exit pressure and $a$ the actual device.

End exams 3 and final only