Specific heat and work:
Continuity (mass conservation):
The first law of thermo (energy conservation):
Work:
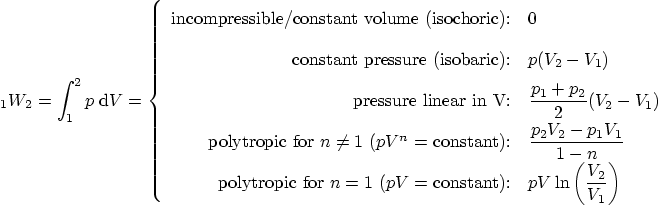
Heat added:

The first law as a rate equation:
Work as a rate equation:
For an ideal gas:
For liquids and solids:
The control volume is assumed to be steady state in all formulae below.
Specific work output and heat added (i.e., per unit mass flowing through):
In- and outflow velocities and pipe cross-sectional areas:
Continuity (mass conservation):
The first law of thermo (energy conservation):