For cycle devices, the normal sign conventions (heat in and work out
are positive) are ignored. Instead, the signs of heat and work are
defined such that ![]() ,
, ![]() and net work
and net work ![]() are
normally positive. The pictures below show the directions of positive
heat fluxes and work rates for a heat engine as compared to a heat
pump (or refrigeration cycle).
are
normally positive. The pictures below show the directions of positive
heat fluxes and work rates for a heat engine as compared to a heat
pump (or refrigeration cycle).
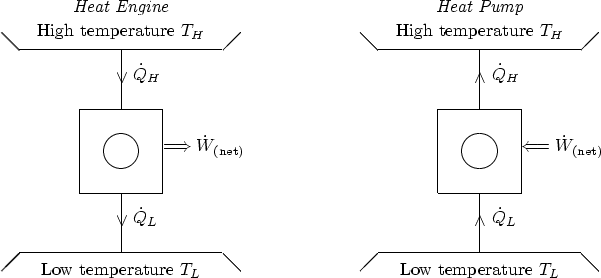
The first law for a cycle:
The Kelvin-Planck Statement: Any working heat engine must dump some waste heat to a lower temperature than the input heat is provided at.
The Clausius Statement: Any working heat pump must have positive work going in.
Thermal efficiency:
Refrigeration coefficient of performance:
Heating heat pump coefficient of performance
![]() :
:
Ideal gas Carnot cycle: