7.1 The Schrö­din­ger Equa­tion

In New­ton­ian me­chan­ics, New­ton's sec­ond law states that the lin­ear mo­men­tum changes in time pro­por­tional to the ap­plied force; ${\rm d}{m}\vec{v}$$\raisebox{.5pt}{$/$}$​${\rm d}{t}$ $\vphantom0\raisebox{1.5pt}{$=$}$ $m\vec{a}$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\vec{F}$. The equiv­a­lent in quan­tum me­chan­ics is the Schrö­din­ger equa­tion, which de­scribes how the wave func­tion evolves. This sec­tion dis­cusses this equa­tion, and a few of its im­me­di­ate con­se­quences.

7.1.1 The equa­tion

The Schrö­din­ger equa­tion says that the time de­riv­a­tive of the wave func­tion is ob­tained by ap­ply­ing the Hamil­ton­ian on it. More pre­cisely:

$$\fbox{$\displaystyle {\rm i}\hbar \frac{\partial \Psi}{\partial t} = H \Psi $} %$$ (7.1)

An equiv­a­lent and ear­lier for­mu­la­tion of quan­tum me­chan­ics was given by Heisen­berg, {A.12}. How­ever, the Schrö­din­ger equa­tion tends to be eas­ier to deal with, es­pe­cially in non­rel­a­tivis­tic ap­pli­ca­tions. An in­te­gral ver­sion of the Schrö­din­ger equa­tion that is some­times con­ve­nient is in {A.13}.

The Schrö­din­ger equa­tions is non­rel­a­tivis­tic. The sim­plest rel­a­tivis­tic ver­sion is called the Klein-Gor­don equa­tion. A dis­cus­sion is in ad­den­dum {A.14}. How­ever, rel­a­tiv­ity in­tro­duces a fun­da­men­tally new is­sue: fol­low­ing Ein­stein’s mass-en­ergy equiv­a­lence, par­ti­cles may be cre­ated out of pure en­ergy or de­stroyed. To deal with that, you typ­i­cally need a for­mu­la­tion of quan­tum me­chan­ics called quan­tum field the­ory. A very brief in­tro­duc­tion is in ad­den­dum {A.15}.

Key Points

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

The Schrö­din­ger equa­tion de­scribes the time evo­lu­tion of the wave func­tion.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

The time de­riv­a­tive is pro­por­tional to the Hamil­ton­ian.

7.1.2 So­lu­tion of the equa­tion

The so­lu­tion to the Schrö­din­ger equa­tion can im­me­di­ately be given for most cases of in­ter­est. The only con­di­tion that needs to be sat­is­fied is that the Hamil­ton­ian de­pends only on the state the sys­tem is in, and not ex­plic­itly on time. This con­di­tion is sat­is­fied in all cases dis­cussed so far, in­clud­ing the par­ti­cle in a box, the har­monic os­cil­la­tor, the hy­dro­gen and heav­ier atoms, and the mol­e­cules, so the fol­low­ing so­lu­tion ap­plies to them all:

To sat­isfy the Schrö­din­ger equa­tion, write the wave func­tion $\Psi$ in terms of what­ever are the en­ergy eigen­func­tions $\psi_{\vec n}$ of the Hamil­ton­ian,

$$\Psi = c_{{\vec n}_1}(t) \psi_{{\vec n}_1} + c_{{\vec n}_2... ...ec n}_2} + \ldots = \sum_{\vec n}c_{\vec n}(t) \psi_{\vec n}$$ (7.2)

Then the co­ef­fi­cients $c_{\vec n}$ must evolve in time as com­plex ex­po­nen­tials:

$$\fbox{$\displaystyle c_{\vec n}(t) = c_{\vec n}(0) e^{-{\rm i}E_{\vec n}t /\hbar} $} %$$ (7.3)

for every com­bi­na­tion of quan­tum num­bers ${\vec n}$.

In short, you get the wave func­tion for ar­bi­trary times by tak­ing the ini­tial wave func­tion and shov­ing in ad­di­tional fac­tors $e^{-{{\rm i}}E_{{\vec n}}t/\hbar}$. The ini­tial val­ues $c_{\vec n}(0)$ of the co­ef­fi­cients are not de­ter­mined from the Schrö­din­ger equa­tion, but from what­ever ini­tial con­di­tion for the wave func­tion is given. As al­ways, the ap­pro­pri­ate set of quan­tum num­bers ${\vec n}$ de­pends on the prob­lem.

Con­sider how this works out for the elec­tron in the hy­dro­gen atom. Here each spa­tial en­ergy state $\psi_{nlm}$ is char­ac­ter­ized by the three quan­tum num­bers $n$, $l$, $m$, chap­ter 4.3. How­ever, there is a spin-up ver­sion $\psi_{nlm}{\uparrow}$ of each state in which the elec­tron has spin mag­netic quan­tum num­ber $m_s$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\frac12$, and a spin-down ver­sion $\psi_{nlm}{\downarrow}$ in which $m_s$ $\vphantom0\raisebox{1.5pt}{$=$}$ $-\frac12$, chap­ter 5.5.1. So the states are char­ac­ter­ized by the set of four quan­tum num­bers

$${\vec n}\equiv (n,l,m,m_s)$$

The most gen­eral wave func­tion for the hy­dro­gen atom is then:

$$\begin{eqnarray*} \lefteqn{\Psi(r,\theta,\phi,S_z,t) =} \\ && \sum_{n=1}^\in... ...) e^{-{\rm i}E_n t/\hbar} \psi_{nlm}(r,\theta,\phi){\downarrow} \end{eqnarray*}$$

Note that each eigen­func­tion has been given its own co­ef­fi­cient that de­pends ex­po­nen­tially on time. (The sum­ma­tion lim­its come from chap­ter 4.3.)

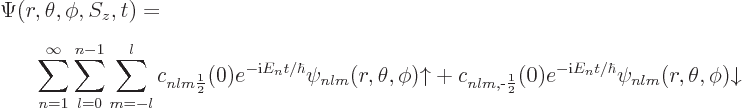
The given so­lu­tion in terms of eigen­func­tions cov­ers most cases of in­ter­est, but as noted, it is not valid if the Hamil­ton­ian de­pends ex­plic­itly on time. That pos­si­bil­ity arises when there are ex­ter­nal in­flu­ences on the sys­tem; in such cases the en­ergy does not just de­pend on what state the sys­tem it­self is in, but also on what the ex­ter­nal in­flu­ences are like at the time.

Key Points

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

Nor­mally, the co­ef­fi­cients of the en­ergy eigen­func­tions must be pro­por­tional to $e^{-{{\rm i}}E_{{\vec n}}t/\hbar}$.

7.1.2 Re­view Ques­tions

1.

The en­ergy of a pho­ton is $\hbar\omega$ where $\omega$ is the clas­si­cal fre­quency of the elec­tro­mag­netic field pro­duced by the pho­ton. So what is $e^{-{{\rm i}}E_{{\vec n}}t/\hbar}$ for a pho­ton? Are you sur­prised by the re­sult?

So­lu­tion schrod­sol-a

2.

For the one-di­men­sion­al har­monic os­cil­la­tor, the en­ergy eigen­val­ues are

$$E_n = \frac{2n+1}{2} \omega$$

Write out the co­ef­fi­cients $c_n(0)e^{-{{\rm i}}E_nt/\hbar}$ for those en­er­gies.

Now clas­si­cally, the har­monic os­cil­la­tor has a nat­ural fre­quency $\omega$. That means that when­ever ${\omega}t$ is a whole mul­ti­ple of $2\pi$, the har­monic os­cil­la­tor is again in the same state as it started out with. Show that the co­ef­fi­cients of the en­ergy eigen­func­tions have a nat­ural fre­quency of $\frac 12\omega$; $\frac 12{\omega}t$ must be a whole mul­ti­ple of $2\pi$ for the co­ef­fi­cients to re­turn to their orig­i­nal val­ues.

So­lu­tion schrod­sol-b

3.

Write the full wave func­tion for a one-di­men­sion­al har­monic os­cil­la­tor. For­mu­lae are in chap­ter 4.1.2.

So­lu­tion schrod­sol-c

7.1.3 En­ergy con­ser­va­tion

The Schrö­din­ger equa­tion im­plies that the en­ergy of a sys­tem is con­served, as­sum­ing that there are no ex­ter­nal in­flu­ences on the sys­tem.

To see why, con­sider the gen­eral form of the wave func­tion:

$$\Psi = \sum_{\vec n}c_{\vec n}(t) \psi_{\vec n} \qquad c_{\vec n}(t) = c_{\vec n}(0) e^{-{\rm i}E_{\vec n}t /\hbar}$$

Ac­cord­ing to chap­ter 3.4, the square mag­ni­tudes $\vert c_{\vec n}\vert^2$ of the co­ef­fi­cients of the en­ergy eigen­func­tions give the prob­a­bil­ity for the cor­re­spond­ing en­ergy. While the co­ef­fi­cients vary with time, their square mag­ni­tudes do not:

$$\vert c_{\vec n}(t)\vert^2 \equiv c_{\vec n}^*(t)c_{\vec n}... ...) e^{-{\rm i}E_{\vec n}t /\hbar} = \vert c_{\vec n}(0)\vert^2$$

So the prob­a­bil­ity of mea­sur­ing a given en­ergy level does not vary with time ei­ther. That means that en­ergy is con­served.

For ex­am­ple, a wave func­tion for a hy­dro­gen atom at the ex­cited en­ergy level $E_2$ might be of the form:

$$\Psi = e^{-{\rm i}E_2 t/\hbar} \psi_{210}{\uparrow}$$

(This cor­re­sponds to an as­sumed ini­tial con­di­tion in which all co­ef­fi­cients $c_{nlmm_s}$ are zero ex­cept $c_{2101}$ $\vphantom0\raisebox{1.5pt}{$=$}$ 1.) The square mag­ni­tude of the ex­po­nen­tial is one, so the en­ergy of this ex­cited atom will stay $E_2$ with 100% cer­tainty for all time. The en­ergy of the atom is con­served.

This is an im­por­tant ex­am­ple, be­cause it also il­lus­trates that an ex­cited atom will stay ex­cited for all time if left alone. That is an ap­par­ent con­tra­dic­tion be­cause, as dis­cussed in chap­ter 4.3, the above ex­cited atom will even­tu­ally emit a pho­ton and tran­si­tion back to the ground state. Even if you put it in a sealed box whose in­te­rior is at ab­solute zero tem­per­a­ture, it will still de­cay.

The ex­pla­na­tion for this ap­par­ent con­tra­dic­tion is that an atom is never truly left alone. Sim­ply put, even at ab­solute zero tem­per­a­ture, quan­tum un­cer­tainty in en­ergy al­lows an elec­tro­mag­netic pho­ton to pop up that per­turbs the atom and causes the de­cay. (To de­scribe more pre­cisely what hap­pens is a ma­jor ob­jec­tive of this chap­ter.)

Re­turn­ing to the un­per­turbed atom, you may won­der what hap­pens to en­ergy con­ser­va­tion if there is un­cer­tainty in en­ergy. In that case, what does not change with time are the prob­a­bil­i­ties of mea­sur­ing the pos­si­ble en­ergy lev­els. As an ar­bi­trary ex­am­ple, the fol­low­ing wave func­tion de­scribes a case of an un­per­turbed hy­dro­gen atom whose en­ergy has a 50/50 chance of be­ing mea­sured as $E_1$, (-13.6 eV), or as $E_2$, (-3.4 eV):

$$\Psi = {\displaystyle\frac{1}{\sqrt2}} e^{-{\rm i}E_1 t/\h... ...\frac{1}{\sqrt2}} e^{-{\rm i}E_2 t/\hbar} \psi_{210}{\uparrow}$$

The 50/50 prob­a­bil­ity ap­plies re­gard­less how long the wait is be­fore the mea­sure­ment is done.

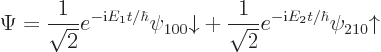
You can turn the ob­ser­va­tions of this sub­sec­tion also around. If an ex­ter­nal ef­fect changes the en­ergy of a sys­tem, then clearly the prob­a­bil­i­ties of the in­di­vid­ual en­er­gies must change. So then the co­ef­fi­cients of the en­ergy eigen­func­tions can­not be sim­ply vary ex­po­nen­tially with time as they do for the un­per­turbed sys­tems dis­cussed above.

Key Points

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

En­ergy con­ser­va­tion is a fun­da­men­tal con­se­quence of the Schrö­din­ger equa­tion.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

An iso­lated sys­tem that has a given en­ergy re­tains that en­ergy.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

Even if there is un­cer­tainty in the en­ergy of an iso­lated sys­tem, still the prob­a­bil­i­ties of the var­i­ous en­er­gies do not change with time.

7.1.4 Sta­tion­ary states

The quest for the dy­nam­i­cal im­pli­ca­tions of the Schrö­din­ger equa­tion must start with the sim­plest case. That is the case in which there is only a sin­gle en­ergy eigen­func­tion in­volved. Then the wave func­tion is of the form

$$\Psi = c_{\vec n}(0) e^{-{\rm i}E_{\vec n}t /\hbar} \psi_{\vec n}$$

Such states are called sta­tion­ary states. Sys­tems in their ground state are of this type.

To see why these states are called sta­tion­ary, note first of all that the en­ergy of the state is $E_{\vec n}$ for all time, with no un­cer­tainty.

But en­ergy is not the only thing that does not change in time. Ac­cord­ing to the Born in­ter­pre­ta­tion, chap­ter 3.1, the square mag­ni­tude of the wave func­tion of a par­ti­cle gives the prob­a­bil­ity of find­ing the par­ti­cle at that po­si­tion and time. Now the square mag­ni­tude of the wave func­tion above is

$$\vert\Psi\vert^2 = \vert\psi_{\vec n}\vert^2$$

Time has dropped out in the square mag­ni­tude; the prob­a­bil­ity of find­ing the par­ti­cle is the same for all time.

For ex­am­ple, con­sider the case of the par­ti­cle in a pipe of chap­ter 3.5. If the par­ti­cle is in the ground state, its wave func­tion is of the form

$$\Psi=c_{111}(0)e^{-{{\rm i}}E_{111}t/\hbar}\psi_{111}$$

The pre­cise form of the func­tion $\psi_{111}$ is not of par­tic­u­lar in­ter­est here, but it can be found in chap­ter 3.5.

The rel­a­tive prob­a­bil­ity for where the par­ti­cle may be found can be shown as grey tones:

Fig­ure 7.1: The ground state wave func­tion looks the same at all times.

The bot­tom line is that this pic­ture is the same for all time.

If the wave func­tion is purely the first ex­cited state $\psi_{211}$, the cor­re­spond­ing pic­ture looks for all time like:

Fig­ure 7.2: The first ex­cited state at all times.

And it is not just po­si­tion that does not change. Nei­ther do lin­ear or an­gu­lar mo­men­tum, ki­netic en­ergy, etcetera. That can be eas­ily checked. The prob­a­bil­ity for a spe­cific value of any phys­i­cal quan­tity is given by

$$\vert\langle\alpha\vert\Psi\rangle\vert^2$$

where $\alpha$ is the eigen­func­tion cor­re­spond­ing to the value. (If there is more than one eigen­func­tion with that value, sum their con­tri­bu­tions.) The ex­po­nen­tial drops out in the square mag­ni­tude. So the prob­a­bil­ity does not de­pend on time.

And if prob­a­bil­i­ties do not change, then nei­ther do ex­pec­ta­tion val­ues, un­cer­tain­ties, etcetera. No phys­i­cally mean­ing­ful quan­tity changes with time.

Hence it is not re­ally sur­pris­ing that none of the en­ergy eigen­func­tions de­rived so far had any re­sem­blance to the clas­si­cal New­ton­ian pic­ture of a par­ti­cle mov­ing around. Each en­ergy eigen­func­tion by it­self is a sta­tion­ary state. There is no change in the prob­a­bil­ity of find­ing the par­ti­cle re­gard­less of the time that you look. So how could it pos­si­bly re­sem­ble a clas­si­cal par­ti­cle that is at dif­fer­ent po­si­tions at dif­fer­ent times?

To get time vari­a­tions of phys­i­cal quan­ti­ties, states of dif­fer­ent en­ergy must be com­bined. In other words, there must be un­cer­tainty in en­ergy.

Key Points

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

States of def­i­nite en­ergy are sta­tion­ary states.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

To get non­triv­ial time vari­a­tion of a sys­tem re­quires un­cer­tainty in en­ergy.

7.1.5 The adi­a­batic ap­prox­i­ma­tion

The pre­vi­ous sub­sec­tions dis­cussed the so­lu­tion for sys­tems in which the Hamil­ton­ian does not ex­plic­itly de­pend on time. Typ­i­cally that means iso­lated sys­tems, un­af­fected by ex­ter­nal ef­fects, or sys­tems for which the ex­ter­nal ef­fects are rel­a­tively sim­ple. If the ex­ter­nal ef­fects pro­duce a time-de­pen­dent Hamil­ton­ian, things get much messier. You can­not sim­ply make the co­ef­fi­cients of the eigen­func­tions vary ex­po­nen­tially in time as done in the pre­vi­ous sub­sec­tions.

How­ever, deal­ing with sys­tems with time-de­pen­dent Hamil­to­ni­ans can still be rel­a­tively easy if the Hamil­ton­ian varies suf­fi­ciently slowly in time. Such sys­tems are quasi-steady ones.

So physi­cists can­not call these sys­tems quasi-steady; that would give the se­cret away to these hated non­spe­cial­ists and pesky stu­dents. For­tu­nately, physi­cists were able to find a much bet­ter name. They call these sys­tems adi­a­batic. That works much bet­ter be­cause the word adi­a­batic is a well-known term in ther­mo­dy­nam­ics: it in­di­cates sys­tems that evolve fast enough that heat con­duc­tion with the sur­round­ings can be ig­nored. So, what bet­ter name to use also for quan­tum sys­tems that evolve slowly enough that they stay in equi­lib­rium with their sur­round­ings? No one fa­mil­iar with even the most ba­sic ther­mo­dy­nam­ics will ever guess what it means.

As a sim­ple ex­am­ple of an adi­a­batic sys­tem, as­sume that you have a par­ti­cle in the ground state in a box. Now you change the vol­ume of the box by a sig­nif­i­cant amount. The ques­tion is, will the par­ti­cle still be in the ground state af­ter the vol­ume change? Nor­mally there is no rea­son to as­sume so; af­ter all, ei­ther way the en­ergy of the par­ti­cle will change sig­nif­i­cantly. How­ever, the “adi­a­batic the­o­rem” says that if the change is per­formed slowly enough, it will. The par­ti­cle will in­deed re­main in the ground state, even though that state slowly changes into a com­pletely dif­fer­ent form.

If the sys­tem is in an en­ergy state other than the ground state, the par­ti­cle will stay in that state as it evolves dur­ing an adi­a­batic process. The the­o­rem does as­sume that the en­ergy is non­de­gen­er­ate, so that the en­ergy state is un­am­bigu­ous. More so­phis­ti­cated ver­sions of the analy­sis ex­ist to deal with de­gen­er­acy and con­tin­u­ous spec­tra.

A de­riva­tion of the the­o­rem can be found in {D.34}. Some ad­di­tional im­pli­ca­tions are in ad­den­dum {A.16}. The most im­por­tant prac­ti­cal ap­pli­ca­tion of the adi­a­batic the­o­rem is with­out doubt the Born-Op­pen­heimer ap­prox­i­ma­tion, which is dis­cussed sep­a­rately in chap­ter 9.2.

Key Points

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

If the prop­er­ties of a sys­tem in its ground state are changed, but slowly, the sys­tem will re­main in the chang­ing ground state.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

More gen­er­ally, the adi­a­batic ap­prox­i­ma­tion can be used to an­a­lyze slowly chang­ing sys­tems.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

No, it has noth­ing to do with the nor­mal use of the word adi­a­batic.